【题目】如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
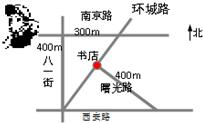
A、600mB、500m
C、400mD、300m
参考答案:
【答案】B
【解析】由于BC∥AD,那么有∠DAE=∠ACB,由题意可知∠ABC=∠DEA=90°,BA=ED,利用AAS可证△ABC≌△DEA,于是AE=BC=300,再利用勾股定理可求AC,即可求CE,根据图可知从B到E的走法有两种,分别计算比较即可.
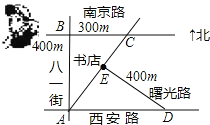
解:如右图所示,
∵BC∥AD,
∴∠DAE=∠ACB,
又∵BC⊥AB,DE⊥AC,
∴∠ABC=∠DEA=90°,
又∵AB=DE=400m,
∴△ABC≌△DEA,
∴EA=BC=300m,
在Rt△ABC中,AC=![]() =500m,
=500m,
∴CE=AC-AE=200,
从B到E有两种走法:①BA+AE=700m;②BC+CE=500m,
∴最近的路程是500m.
故选B.
本题考查了平行线的性质、全等三角形的判定和性质、勾股定理.解题的关键是证明△ABC≌△DEA,并能比较从B到E有两种走法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,

(1)求抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,写出自变量x的取值范围,并求当x取多少时,S的值最大,最大是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填表:
a
0.000 001
0.001
1
1 000
1 000 000
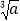
0.01
0.1
1
10
100
(2)由上表你发现了什么规律?请用语言叙述这个规律:被开方数扩大_____;
(3)根据你发现的规律填空:
①已知
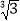 =1.442,则
=1.442,则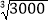 =______,
=______,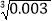 =______;
=______;②已知
 =0.076 97,则=______.
=0.076 97,则=______. -
科目: 来源: 题型:
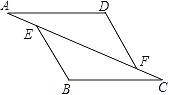
查看答案和解析>>【题目】如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.
(1)AD与BC相等吗?请说明理由;
(2)BE与DF平行吗?请说明理由.
-
科目: 来源: 题型:
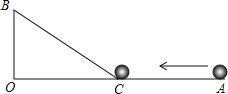
查看答案和解析>>【题目】如图,∠AOB=90°,OA=45cm,OB=15cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
-
科目: 来源: 题型:
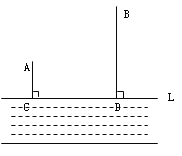
查看答案和解析>>【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A.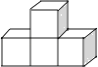
B.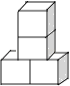
C.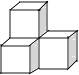
D.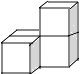
相关试题

