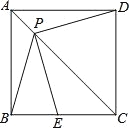
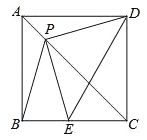
【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
参考答案:
【答案】(1)详见解析;(2)∠PED=45°,证明见解析.
【解析】
试题分析:(1)根据正方形的性质四条边都相等可得BC=CD,对角线平分一组对角线可得∠ACB=∠ACD,然后利用“边角边”证明△PBC和△PDC全等,根据全等三角形对应边相等可得PB=PD,然后等量代换即可得证;(2)根据全等三角形对应角相等可得∠PBC=∠PDC,根据等边对等角可得∠PBC=∠PEB,从而得到∠PDC=∠PEB,再根据∠PEB+∠PEC=180°求出∠PDC+∠PEC=180°,然后根据四边形的内角和定理求出∠DPE=90°,判断出△PDE是等腰直角三角形,根据等腰直角三角形的性质求解即可.
试题解析:(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠ACB=∠ACD,
在△PBC和△PDC中,
 ,
,
∴△PBC≌△PDC(SAS),
∴PB=PD,
∵PE=PB,
∴PE=PD;
(2)判断∠PED=45°.
证明:∵四边形ABCD是正方形,
∴∠BCD=90°,
∵△PBC≌△PDC,
∴∠PBC=∠PDC,
∵PE=PB,
∴∠PBC=∠PEB,
∴∠PDC=∠PEB,
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
在四边形PECD中,∠EPD=360°﹣(∠PDC+∠PEC)﹣∠BCD=360°﹣180°﹣90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形,
∴∠PED=45°.
-
科目: 来源: 题型:
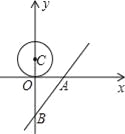
查看答案和解析>>【题目】在平面直角坐标系中,点C的坐标为(0,1.5),我们把以点C为圆心,半径为1.5的圆称为点C的朋友圈,圆周上的每一个点叫做点C的一个好友.
(1)写出点C的两个好友坐标;
(2)直线l的解析式是y=
 x﹣4,与x轴、y轴分别交于A、B两点,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当点C的朋友圈有好友落在直线上时,直线将受其影响,求在点C向下运动的过程中,直线受其影响的时间;
x﹣4,与x轴、y轴分别交于A、B两点,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当点C的朋友圈有好友落在直线上时,直线将受其影响,求在点C向下运动的过程中,直线受其影响的时间;(3)抛物线y=ax2+bx+c过原点O和点A,且顶点D恰好为点C的好友,连接OD.E为⊙C上一点,当△DOE面积最大时,求点E的坐标,此时△DOE的面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断下面两句话是否正确.若正确请说明理由;若不正确,请举例说明.
(1)两个实数的和一定大于每一个加数.
(2)两个无理数的积一定是无理数. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简x+y﹣(x﹣y)的最后结果是( )
A. 2x+2y B. 2y C. 2x D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C在平面直角坐标系中的坐标分别为(5,5),(3,2),(6,3).
(1)作△ABC关于直线l:x=1对称的△A1B1C1,点A,B,C的对称点分别是A1,B1,C1;
(2)点A1的坐标为__________,
点B1的坐标为__________,
点C1的坐标为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一条信息在一周内被转发了2180000次,将数据2180000用科学记数法表示为( )
A. 2.18×105 B. 2.18×106 C. 21.8×106 D. 21.8×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.
(1)求证:AC是⊙O的切线;
(2)若sinC=
 ,AC=6,求⊙O的直径.
,AC=6,求⊙O的直径.
相关试题

