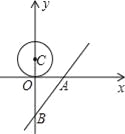
【题目】在平面直角坐标系中,点C的坐标为(0,1.5),我们把以点C为圆心,半径为1.5的圆称为点C的朋友圈,圆周上的每一个点叫做点C的一个好友.
(1)写出点C的两个好友坐标;
(2)直线l的解析式是y=![]() x﹣4,与x轴、y轴分别交于A、B两点,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当点C的朋友圈有好友落在直线上时,直线将受其影响,求在点C向下运动的过程中,直线受其影响的时间;
x﹣4,与x轴、y轴分别交于A、B两点,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当点C的朋友圈有好友落在直线上时,直线将受其影响,求在点C向下运动的过程中,直线受其影响的时间;
(3)抛物线y=ax2+bx+c过原点O和点A,且顶点D恰好为点C的好友,连接OD.E为⊙C上一点,当△DOE面积最大时,求点E的坐标,此时△DOE的面积是多少?
参考答案:
【答案】(1)点(0,0)、(0,3)为点C的好友;(2)在点C向下运动的过程中,直线受其影响的时间为6≤t≤16;(3)当△DOE面积最大时,点E的坐标为(﹣![]() ,
, ![]() ),此时△DOE的面积是
),此时△DOE的面积是![]() .
.
【解析】试题分析:(1)由朋友圈以及好友的定义,结合图形,即可得出结论;(2)设圆心C往下运动了t秒,则点C的坐标为(0,1.5﹣0.5t),根据好友的定义,结合点C到直线l的距离小于等于1.5,即可得出关于时间t的含绝对值符号的一元一次方程,解方程即可得出结论;(3)根据二次函数的性质找出抛物线的对称轴,结合函数图象以及好友的定义找出点D的坐标;连接OD,过点C作CM⊥OD于点M,延长MC交圆C于点E,连接EO、ED,通过垂径定理、解直角三角形求出线段EM的长,再结合三角形的面积公式即可求出S△DOE的值,由点C、M点的坐标利用待定系数法求出直线CM的解析式,设出点E的坐标,再结合两点间的距离公式即可求出点E的坐标,此题得解.
试题解析:(1)1.5﹣1.5=0,1.5+1.5=3,
∴点(0,0)、(0,3)到点C的距离为1.5,
∴点(0,0)、(0,3)为点C的好友.
(2)设圆心C往下运动了t秒,则点C的坐标为(0,1.5﹣0.5t),
直线l:y=![]() x﹣4可变形为4x﹣3y﹣12=0,
x﹣4可变形为4x﹣3y﹣12=0,
点C到直线l的距离d=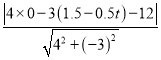 =|0.3t﹣3.3|,
=|0.3t﹣3.3|,
当直线受圆C影响时,有d≤1.5,即|0.3t﹣3.3|≤1.5,
解得:6≤t≤16.
∴在点C向下运动的过程中,直线受其影响的时间为6≤t≤16.
(3)令y=![]() x﹣4中y=0,则
x﹣4中y=0,则![]() x﹣4=0,
x﹣4=0,
解得:x=3,即点A的坐标为(3,0).
依照题意画出图形,如图1所示.
∵抛物线y=ax2+bx+c过原点O和点A,点O(0,0),点A(3,0),
∴抛物线的对称轴为x=![]() =1.5,
=1.5,
∵点D恰好为点C的好友,
∴点D的坐标为(1.5,1.5).
连接OD,过点C作CM⊥OD于点M,延长MC交圆C于点E,连接EO、ED,此时S△DOE最大,如图2所示.
∵OD是圆C的弦,CM⊥OD,
∴点M为线段OD的中点,
∴点M的坐标为(![]() ,
, ![]() )、OM=
)、OM=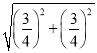 =
=![]() ,
,
在Rt△CMO中,OM=![]() ,CO=1.5=
,CO=1.5=![]() ,
,
∴CM=![]() =
=![]() .
.
∵CE=1.5=![]() ,EM=EC+CM,
,EM=EC+CM,
∴EM=![]() ,
,
此时S△DOE=![]() ODEM=OMEM=
ODEM=OMEM=![]() ×
×![]() =
=![]() .
.
设直线CM的解析式为y=mx+n,
∵点C的坐标为(0,1.5)、点M的坐标为(![]() ,
, ![]() )即(0.75,0.75),
)即(0.75,0.75),
∴![]() ,解得:
,解得: ![]() ,
,
∴直线CM的解析式为y=﹣x+1.5.
设点E的坐标为(x,﹣x+1.5)(x<0),
∵EC=![]() =1.5,
=1.5,
∴x=﹣![]() ,或x=
,或x=![]() (舍去),
(舍去),
∴点E的坐标为(﹣![]() ,
, ![]() ).
).
故当△DOE面积最大时,点E的坐标为(﹣![]() ,
, ![]() ),此时△DOE的面积是
),此时△DOE的面积是![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC.
(1)求证:AB是⊙O的切线;
(2)若PC=
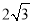 ,OA=3,求⊙O的半径和线段PB的长.
,OA=3,求⊙O的半径和线段PB的长.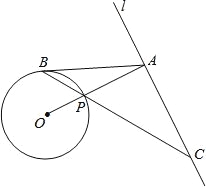
-
科目: 来源: 题型:
查看答案和解析>>【题目】平方等于16的数是___________,立方等于27的数是___________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学规定学生的学期体育总评成绩满分为100分,其中平均成绩占20%,期中考试成绩占30%,期末考试成绩占50%,小彤的三项成绩(百分制)依次为95,90,88,则小彤这学期的体育总评成绩为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断下面两句话是否正确.若正确请说明理由;若不正确,请举例说明.
(1)两个实数的和一定大于每一个加数.
(2)两个无理数的积一定是无理数. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简x+y﹣(x﹣y)的最后结果是( )
A. 2x+2y B. 2y C. 2x D. 0
-
科目: 来源: 题型:
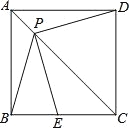
查看答案和解析>>【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
相关试题

