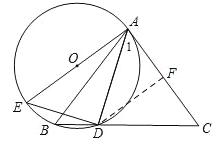
【题目】如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.
(1)求证:AC是⊙O的切线;
(2)若sinC=![]() ,AC=6,求⊙O的直径.
,AC=6,求⊙O的直径.

参考答案:
【答案】(1)详见解析;(2)⊙O的直径为![]() .
.
【解析】试题分析:(1)根据等腰三角形的性质,由AB=AC,AD=DC得∠C=∠B,∠1=∠C,则∠1=∠B,根据圆周角定理得∠E=∠B,∠ADE=90°,所以∠1+∠EAD=90°,然后根据切线的判定定理即可得到AC是⊙O的切线;
(2)过点D作DF⊥AC于点F,如图,根据等腰三角形的性质得CF=![]() AC=3,在Rt△CDF中,利用正弦定义得sinC=
AC=3,在Rt△CDF中,利用正弦定义得sinC=![]() =
=![]() ,则设DF=4x,DC=5x,利用勾股定理得CF=3x,所以3x=3,解得x=1,于是得到DC=AD=5,然后证明△ADE∽△DFC,再利用相似比可计算AE即可.
,则设DF=4x,DC=5x,利用勾股定理得CF=3x,所以3x=3,解得x=1,于是得到DC=AD=5,然后证明△ADE∽△DFC,再利用相似比可计算AE即可.
试题解析:(1)∵AB=AC,AD=DC,
∴∠C=∠B,∠1=∠C,
∴∠1=∠B,
又∵∠E=∠B,
∴∠1=∠E,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠E+∠EAD=90°,
∴∠1+∠EAD=90°,即∠EAC=90°,
∴AE⊥AC,
∴AC是⊙O的切线;
(2)过点D作DF⊥AC于点F,如图,
∵DA=DC,
∴CF=![]() AC=3,
AC=3,
在Rt△CDF中,∵sinC=![]() =
=![]() ,
,
设DF=4x,DC=5x,
∴CF=![]() =3x,
=3x,
∴3x=3,解得x=1,
∴DC=5,
∴AD=5,
∵∠ADE=∠DFC=90°,∠E=∠C,
∴△ADE∽△DFC,
∴![]() ,即
,即![]() ,解得AE=
,解得AE=![]() ,
,
即⊙O的直径为![]() .
.
-
科目: 来源: 题型:
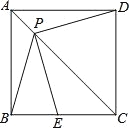
查看答案和解析>>【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C在平面直角坐标系中的坐标分别为(5,5),(3,2),(6,3).
(1)作△ABC关于直线l:x=1对称的△A1B1C1,点A,B,C的对称点分别是A1,B1,C1;
(2)点A1的坐标为__________,
点B1的坐标为__________,
点C1的坐标为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一条信息在一周内被转发了2180000次,将数据2180000用科学记数法表示为( )
A. 2.18×105 B. 2.18×106 C. 21.8×106 D. 21.8×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC中:
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).

-
科目: 来源: 题型:
查看答案和解析>>【题目】神舟十号飞船是我国“神州”系列飞船之一,每小时飞行约28000公里,将28000用科学记数法表示应为公里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的每一个内角都相等,且每一个内角的度数为135°,那么这个多边形的边数为( )
A. 6 B. 7 C. 8 D. 以上答案都不对
相关试题

