【题目】小明遇到下面的问题:求代数式![]() 的最小值并写出取到最小值时的x值.经过观察式子结构特征,小明联想到可以用解一元二次方程中的配方法来解决问题,具体分析过程如下:
的最小值并写出取到最小值时的x值.经过观察式子结构特征,小明联想到可以用解一元二次方程中的配方法来解决问题,具体分析过程如下:
![]() ,所以,当x=1 时,代数式有最小值是-4.
,所以,当x=1 时,代数式有最小值是-4.
(1)请你用上面小明思考问题的方法解决下面问题.
① ![]() 的最小值是_______;②求
的最小值是_______;②求![]() 的最小值.
的最小值.
(2)小明受到上面问题的启发,自己设计了一个问题,并给出解题过程及结论如下:
问题:当x为实数时,求![]() 的最小值.
的最小值.
解:![]() ,∴原式有最小值是5.
,∴原式有最小值是5.
请你判断小明的结论是否正确,并简要说明理由.
判断:__________,理由:____________________________________________________.
参考答案:
【答案】(1)①-9②4(2)小明的结论错误
【解析】分析:1)①根据题意可以将式子化为题目中例子中的形式,从而可以解答本题;②根据题意可以将式子化为题目中例子中的形式,从而可以解答本题;
(2)根据题目中的式子可以得到小明的做法是否正确.
详解:(1)①x2-6x=x2-6x+9-9=(x-3)2-9,
∴当x=1时,代数式x2-6x有最小值是-9;
②x2-4x+y2+2y+9=x2-4x+4+y2+2y+1+4=(x-2)2+(y+1)2+4,
∴当x=2,y=-1时,代数式x2-4x+y2+2y+5有最小值是4,
(2)小明的结论错误,
理由:∵x2+1=0时,x无解,
∴(x2+1)2+5最小值不是5,
∵x2≥0,∴当x2=0时,(x2+1)2+5最小值是6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】贾宪三角(如图)最初于11世纪被发现,原图(图2左)载于我国北宋时期数学家贾宪的著作中.这一成果比国外领先600年!这个三角形的构造法则是:两腰都是1,其余每个数为其上方左右两数之和.它给出(a+b)n(n为正整数)展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应着
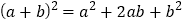 的展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
的展开式中的系数;第四行的四个数1,3,3,1,恰好对应着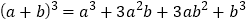 展开式中的系数;等等.
展开式中的系数;等等.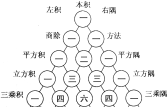

(1)请根据贾宪三角直接写出
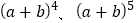 的展开式:
的展开式: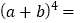 .
.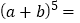 .
.(2)请用多项式乘法或所学的乘法公式验证你写出的
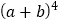 的结果.
的结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用火柴棒按以下方式搭小鱼,是课本上多次出现的数学活动.

(1)搭4条小鱼需要火柴棒_________根;
(2)搭n条小鱼需要火柴棒_____________根;
(3)若搭n朵某种小花需要火柴棒(3n+44)根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
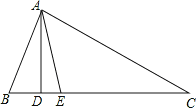
(1)∠BAE的度数;
(2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=
 ,tan
,tan 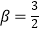 ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 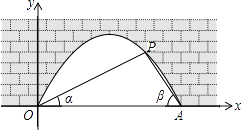
(1)求点P的坐标;
(2)水面上升1m,水面宽多少(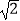 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)? -
科目: 来源: 题型:
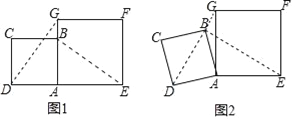
查看答案和解析>>【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为
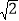 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.(1)小明发现DG⊥BE,请你帮他说明理由;
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数
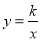 (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).(1)求这个反比例函数的表达式;
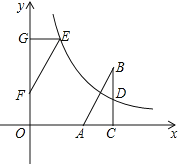
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
相关试题

