【题目】如图,用火柴棒按以下方式搭小鱼,是课本上多次出现的数学活动.

(1)搭4条小鱼需要火柴棒_________根;
(2)搭n条小鱼需要火柴棒_____________根;
(3)若搭n朵某种小花需要火柴棒(3n+44)根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
参考答案:
【答案】(1)26;(2)6n+2;(3)m=14,有86条.
【解析】
(1)根据图形可得后一个图形中火柴数量是前一个图形火柴数量加6;
(2)根据题意找出规律即可得出结论;
(3)根据题意得6m+2=3m+44,可得答案.
(1)根据图形可得后一个图形中火柴数量是前一个图形火柴数量加6,根据题意,求出搭4条小鱼需要用6×4+2根火柴棒,即26根;
(2)第一个小鱼需要8根火柴棒,
第二个小鱼需要14根火柴棒,
第三个小鱼需要20根火柴棒;
∴每个小鱼比前一个小鱼多用6根火柴棒,
∴搭n条小鱼需要用8+6(n1)=(6n+2)根火柴棒.
故答案为:6n+2;
(3)由已知可得3m+44 = 2+6m,解得m=14,火柴总数=2+6×14=86.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款. 乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔买水性笔的费用.
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
-
科目: 来源: 题型:
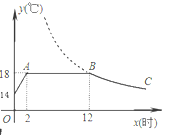
查看答案和解析>>【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=
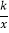 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当棚内温度不低于16℃时,该蔬菜能够快速生长,请问这天该蔬菜能够快速生长多长时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】贾宪三角(如图)最初于11世纪被发现,原图(图2左)载于我国北宋时期数学家贾宪的著作中.这一成果比国外领先600年!这个三角形的构造法则是:两腰都是1,其余每个数为其上方左右两数之和.它给出(a+b)n(n为正整数)展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应着
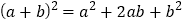 的展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
的展开式中的系数;第四行的四个数1,3,3,1,恰好对应着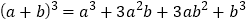 展开式中的系数;等等.
展开式中的系数;等等.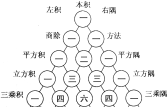

(1)请根据贾宪三角直接写出
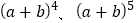 的展开式:
的展开式: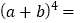 .
.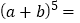 .
.(2)请用多项式乘法或所学的乘法公式验证你写出的
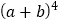 的结果.
的结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
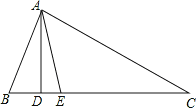
(1)∠BAE的度数;
(2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明遇到下面的问题:求代数式
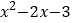 的最小值并写出取到最小值时的x值.经过观察式子结构特征,小明联想到可以用解一元二次方程中的配方法来解决问题,具体分析过程如下:
的最小值并写出取到最小值时的x值.经过观察式子结构特征,小明联想到可以用解一元二次方程中的配方法来解决问题,具体分析过程如下: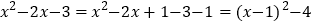 ,所以,当x=1 时,代数式有最小值是-4.
,所以,当x=1 时,代数式有最小值是-4.(1)请你用上面小明思考问题的方法解决下面问题.
①
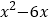 的最小值是_______;②求
的最小值是_______;②求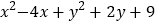 的最小值.
的最小值.(2)小明受到上面问题的启发,自己设计了一个问题,并给出解题过程及结论如下:
问题:当x为实数时,求
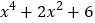 的最小值.
的最小值.解:
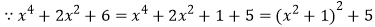 ,∴原式有最小值是5.
,∴原式有最小值是5.请你判断小明的结论是否正确,并简要说明理由.
判断:__________,理由:____________________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=
 ,tan
,tan 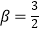 ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 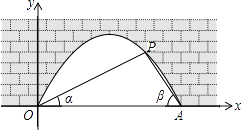
(1)求点P的坐标;
(2)水面上升1m,水面宽多少(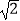 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
相关试题

