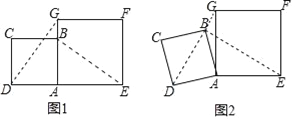
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为![]() 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
(1)小明发现DG⊥BE,请你帮他说明理由;
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
参考答案:
【答案】(1)见解析 (2)![]() +
+![]()
【解析】分析:(1)延长EB交DG于点H,先证出Rt△ADG≌Rt△ABE,得出∠AGD=∠AEB,再根据∠HBG=∠EBA,得出∠HGB+∠HBG=90°即可;
(2)过点A作AP⊥BD交BD于点P,根据△DAG≌△BAE得出DG=BE,根据AD=2∠PDA=45°,∠APD=90°,求出AP、DP,利用勾股定理求出PG,再根据DG=DP+PG求出DG,最后根据DG=BE即可得出答案.
详解:(1)如图1,延长EB交DG于点H,
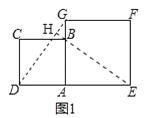
∵ABCD和AEFG为正方形,
∴在Rt△ADG和Rt△ABE中,
 ,
,
∴Rt△ADG≌Rt△ABE,
∴∠AGD=∠AEB,
∵∠HBG=∠EBA,
∴∠HGB+∠HBG=90°,
∴DG⊥BE;
(2)如图2,过点A作AP⊥BD交BD于点P,
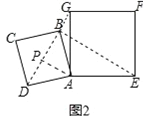
∵ABCD和AEFG为正方形,
∴在△DAG和△BAE中,
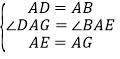 ,
,
∴△DAG≌△BAE(SAS),
∴DG=BE,
∵AD=2∠PDA=45°,∠APD=90°,
∴AP=DP=![]() ,
,
∵AG=2![]() ,∴PG=
,∴PG=![]() =
=![]() ,
,
∴DG=DP+PG=![]() +
+![]() ,
,
∵DG=BE,∴BE=![]() +
+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
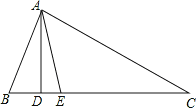
(1)∠BAE的度数;
(2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明遇到下面的问题:求代数式
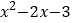 的最小值并写出取到最小值时的x值.经过观察式子结构特征,小明联想到可以用解一元二次方程中的配方法来解决问题,具体分析过程如下:
的最小值并写出取到最小值时的x值.经过观察式子结构特征,小明联想到可以用解一元二次方程中的配方法来解决问题,具体分析过程如下: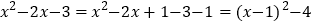 ,所以,当x=1 时,代数式有最小值是-4.
,所以,当x=1 时,代数式有最小值是-4.(1)请你用上面小明思考问题的方法解决下面问题.
①
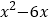 的最小值是_______;②求
的最小值是_______;②求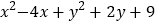 的最小值.
的最小值.(2)小明受到上面问题的启发,自己设计了一个问题,并给出解题过程及结论如下:
问题:当x为实数时,求
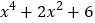 的最小值.
的最小值.解:
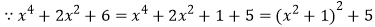 ,∴原式有最小值是5.
,∴原式有最小值是5.请你判断小明的结论是否正确,并简要说明理由.
判断:__________,理由:____________________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=
 ,tan
,tan 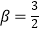 ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 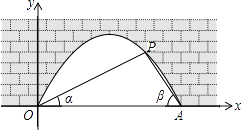
(1)求点P的坐标;
(2)水面上升1m,水面宽多少(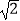 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)? -
科目: 来源: 题型:
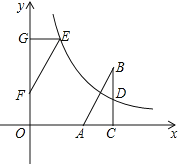
查看答案和解析>>【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数
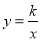 (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,信丰县某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形圆心角是 度;
(2)请补全条形统计图;
(3)若该中学共有学生1200人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?

相关试题

