【题目】已知关于x的方程(m-1)x2-x-2=0.
(1)若x=-1是方程的一个根,求m的值和方程的另一根;
(2)当m为何实数时,方程有两个不相等的实数根?
(3)若x1,x2是方程的两个实数根,且xx2+x1x=-![]() ,试求实数m的值.
,试求实数m的值.
参考答案:
【答案】(1) x=2;(2)方程有两个不相等的实数根;(3) m=5.
【解析】(1)把x=-1代入方程可求得m,再解方程可求另一根;(2)当Δ=(-1)2-4×(m-1)×(-2)=8m-7>0时,方程有两个不相等的实数根;(3)根据根与系数关系可得:x12x2+x1x22=x1x2(x1+x2)=![]() ,进一步可求的m.
,进一步可求的m.
解:(1)∵x=-1是方程的一个根,
∴m-1+1-2=0,则m=2,
∴原方程为x2-x-2=0,解得x1=2,x2=-1.
∴m=2,方程的另一根是x=2;
(2)依题意得Δ=(-1)2-4×(m-1)×(-2)=8m-7>0,
∴m>![]() .
.
又∵m-1≠0,
∴m≠1.
故当m>![]() 且m≠1时,
且m≠1时,
方程有两个不相等的实数根;
(3)x12x2+x1x22=x1x2(x1+x2)=![]() ,
,
∴(m-1)2=16,
∴m1=5,m2=-3.
∵方程有两个实数根,
∴Δ=8m-7≥0,
∴m≥![]() ,且m≠1.
,且m≠1.
∴m=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C分别是线段A1B、B1C、C1A的中点,若△A1BlC1的面积是14,那么△ABC的面积是( )

A.2B.
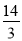 C.3D.
C.3D.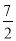
-
科目: 来源: 题型:
查看答案和解析>>【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
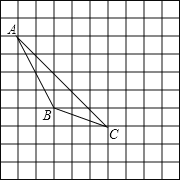
查看答案和解析>>【题目】如图,每个小正方形的边长均为1,每个小方格的顶点叫格点
(1)画出△ABC中AB边上的中线CD;
(2)画出△ABC向右平移4个单位后得到的△A1B1C1;
(3)图中AC与A1C1的关系是:______;
(4)S△ABC的面积是______.
-
科目: 来源: 题型:
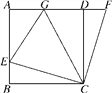
查看答案和解析>>【题目】如图,在正方形ABCD中,E是AB边上一点,F是AD延长线上一点,BE=DF.
(1)求证:CE=CF;
(2)若点G在AD边上,且∠GCE=45°,BE=3,DG=5,求GE的长.
-
科目: 来源: 题型:
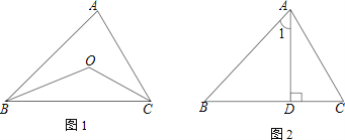
查看答案和解析>>【题目】(1)如图1,△ABC中,∠BAC=60°,内角∠ABC、∠ACB的平分线相交于点O,则∠BOC=______;
(2)如图2,△ABC中,∠BAC=60°,AD是△ABC的边BC上的高,且∠B=∠1,求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是双曲线y=﹣
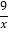 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=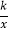 上运动,则k的值为( )
上运动,则k的值为( )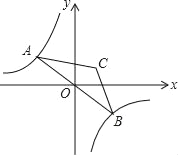
A. 3 B. 4 C. 2.5 D. 7
相关试题

