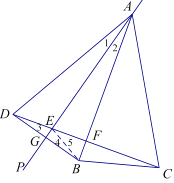
【题目】如图,已知等腰△ABC中,∠BAC=30°,AB=AC,∠PAB=α,点B关于直线AP的对称点为点D,连接AD,连接BD交AP于点G,连接CD交AP于点E,交AB于点F.
(1)如图当α=15°时,①按要求画出图形,②求出∠ACD的度数,③探究DE与BF的倍数关系并加以证明;
(2)在直线AP绕点A顺时针旋转的过程中(0°<α<75°),当△AEF为等腰三角形时,画出相应图形直接求出α的值为________.

参考答案:
【答案】(1)①见解析;②∠ACD=60°;③DE=2BF,理由见解析;(2)30°或52.5°.
【解析】
(1)①按要求画出即可;
②根据点B关于直线AP的对称点为点D,得到AP垂直平分BD,利用垂直平分线的性质,证明△ACD为等边三角形,即可得到∠ACD=60°;
③DE=2BF,连接EB,根据AP垂直平分BD,得到ED=EB,利用等边对等角得到∠3=∠4,利用等腰三角形的性质求出∠3=∠4=15°,∠5=30°,又因为AD=AC,AB平分∠DAC,所以AB⊥DC,即可得到EB=2BF,所以ED=2BF;
(2)画出图形,分三种情况讨论:当AE=AF时;当AE=EF时;当EF=AF时.
(1)①如图为所求作的图形;
②∵ B、D关于AP对称,
∴AP垂直平分BD,AD=AB,∠1=∠2=15°,
∴∠DAC=60°,
∴△ACD为等边三角形,
∴∠ACD=60°;
③ DE=2BF ,理由如下:
连接 EB,
∴ED=EB,
∵AB=AD,∠DAB=30°,
∴∠ADB=75°,
又∵∠ADC=60°,
∴∠3=∠4=15°,
∴∠5=30°,
∵AD=AC ,
AB平分∠DAC ,
∴AB⊥DC ,
∴EB=2BF,
∴ED=2BF ;
(2)如图2,
∵AD=AC,
∴△DAC是等腰三角形,
∴∠ADC=(180°-2α-30°)÷2=75°-α,
∴∠AEF=∠ADC+∠DAE=75°-α+α=75°,
当AE=AF时,∠EAF=α=180°-75°×2=180°-150°=30°;
当AE=EF时,∠EAF=α=(180°-75°)÷=52.5°;
当EF=AF时,∠AEF=∠EAF=a=75°(舍去),
故答案为:30°或52.5°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,AB=BC,∠ABC=90°,F 为 AB 延长线上一点,点 E 在BC 上,且 AE=CF.

(1)求证: AE⊥CF;
(2)若∠CAE=25°,求∠ACF 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下面例题,解答问题:例题: 已知二次三项式x2 4x m 有一个因式是 ( x 3) ,求另一个因式以及 m 的值.
解:设另一个因式为 ( x n) ,得x2 4x m ( x 3) ( x n)
则x2 4 x m x2 (n 3) x 3n
∴

解得: n 7, m 21
∴ 另一个因式为 ( x 7) , m 的值为-21 .
问题:仿照以上方法解答下面问题:
(1)已知二次三项式2x2+3x-k有一个因式是(2x-5),求另一个因式以及k的值.
(2)已知二次三项式6x2+4ax+2有一个因式是(2x+a),a是正整数,求另一个因式以及a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列各题:
(1)先化简,再求代数式(
 的值,其中x=
的值,其中x= cos30°+
cos30°+ ;
;(2)已知α是锐角,且sin(α+15°)=
 .计算
.计算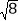 -4cosα-(π-3.14)0+tanα+(
-4cosα-(π-3.14)0+tanα+( )-1的值.
)-1的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明遇到一个问题:已知:如图1,在△ABC中,∠BAC=120°,∠ABC=40°,试过△ABC的一个顶点画一条直线,将此三角形分割成两个等腰三角形.
他的做法是:如图2,首先保留最小角∠C,然后过三角形顶点A画直线交BC于点D. 将∠BAC分成两个角,使∠DAC=20°,△ABC即可被分割成两个等腰三角形.
喜欢动脑筋的小明又继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
他的做法是:

如图3,先画△ADC ,使DA=DC,延长AD到点B,使△BCD也是等腰三角形,如果DC=BC,那么∠CDB =∠ABC,因为∠CDB=2∠A,所以∠ABC= 2∠A.于是小明得到了一个结论:
当三角形中有一个角是最小角的2倍时,则此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
请你参考小明的做法继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.请直接写出你所探究出的另外两条结论(不必写出探究过程或理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC﹣AB=2BE中正确的是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列各题:
(1)已知∠A,∠B,∠C是锐角三角形ABC的三个内角,且满足(2sinA-
 )2+
)2+ =0,求∠C的度数;
=0,求∠C的度数;(2)已知tanα的值是方程x2-x-2=0的一个根,求式子
 的值.
的值.
相关试题

