【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC﹣AB=2BE中正确的是_____.

参考答案:
【答案】①②④
【解析】
利用“HL”证明Rt△BDE和Rt△CDF全等,根据全等三角形对应边相等可得DE=DF,再根据到角的两边距离相等的点在角的平分线上判断出AD平分∠BAC,然后利用“HL”证明Rt△ADE和Rt△ADF全等,根据全等三角形对应边相等可得AE=AF,再根据图形表示出表示出AE、AF,再整理即可得到AC﹣AB=2BE.
解:在Rt△BDE和Rt△CDF中,
![]() ,
,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF,故①正确;
又∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC,故②正确;
在Rt△ADE和Rt△ADF中,
![]() ,
,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,
∴AB+BE=AC﹣FC,
∴AC﹣AB=BE+FC=2BE,
即AC﹣AB=2BE,故④正确;
由垂线段最短可得AE<AD,故③错误,
综上所述,正确的是①②④.
故答案为:①②④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列各题:
(1)先化简,再求代数式(
 的值,其中x=
的值,其中x= cos30°+
cos30°+ ;
;(2)已知α是锐角,且sin(α+15°)=
 .计算
.计算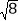 -4cosα-(π-3.14)0+tanα+(
-4cosα-(π-3.14)0+tanα+( )-1的值.
)-1的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC中,∠BAC=30°,AB=AC,∠PAB=α,点B关于直线AP的对称点为点D,连接AD,连接BD交AP于点G,连接CD交AP于点E,交AB于点F.
(1)如图当α=15°时,①按要求画出图形,②求出∠ACD的度数,③探究DE与BF的倍数关系并加以证明;
(2)在直线AP绕点A顺时针旋转的过程中(0°<α<75°),当△AEF为等腰三角形时,画出相应图形直接求出α的值为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明遇到一个问题:已知:如图1,在△ABC中,∠BAC=120°,∠ABC=40°,试过△ABC的一个顶点画一条直线,将此三角形分割成两个等腰三角形.
他的做法是:如图2,首先保留最小角∠C,然后过三角形顶点A画直线交BC于点D. 将∠BAC分成两个角,使∠DAC=20°,△ABC即可被分割成两个等腰三角形.
喜欢动脑筋的小明又继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
他的做法是:

如图3,先画△ADC ,使DA=DC,延长AD到点B,使△BCD也是等腰三角形,如果DC=BC,那么∠CDB =∠ABC,因为∠CDB=2∠A,所以∠ABC= 2∠A.于是小明得到了一个结论:
当三角形中有一个角是最小角的2倍时,则此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
请你参考小明的做法继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.请直接写出你所探究出的另外两条结论(不必写出探究过程或理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列各题:
(1)已知∠A,∠B,∠C是锐角三角形ABC的三个内角,且满足(2sinA-
 )2+
)2+ =0,求∠C的度数;
=0,求∠C的度数;(2)已知tanα的值是方程x2-x-2=0的一个根,求式子
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,

(1)求证:△ABE≌△BCD;
(2)求出∠AFB的度数.
-
科目: 来源: 题型:
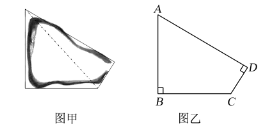
查看答案和解析>>【题目】如图是我国某海域内的一个小岛,其平面图如图甲所示,小明据此构造出该岛的一个数学模型如图乙所示,其中∠B=∠D=90°,AB=BC=15千米,CD=3
 千米,请据此解答如下问题:
千米,请据此解答如下问题:(1)求该岛的周长和面积;(结果保留整数,参考数据:
 ≈1.414,
≈1.414, ≈1.732,
≈1.732, ≈2.449)
≈2.449)(2)求∠ACD的余弦值.
相关试题

