【题目】我县某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图1所示,(单位:cm)
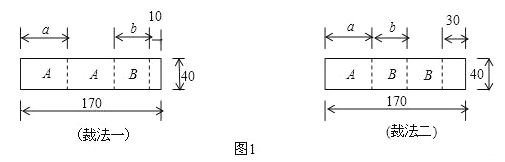
(1)列出方程(组),求出图甲中a与b的值.
(2)在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图2的竖式与横式两种无盖礼品盒.
①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒x个,横式无盖礼品盒的y个,根据题意完成表格:
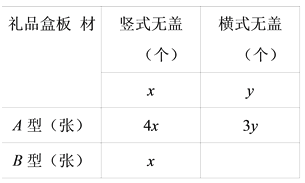
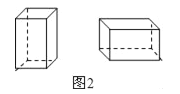
③做成的竖式和横式两种无盖礼品盒总数最多是 个;此时,横式无盖礼品盒可以做 个.(在横线上直接写出答案,无需书写过程)
参考答案:
【答案】(1)a=60,b=40;(2)①64,38;②2y;③20,16或17或18.
【解析】
(1)由图示列出关于a、b的二元一次方程组求解;
(2)根据已知和图示计算出两种裁法共产生A型板材和B型板材的张数,同样由图示完成表格,并完成计算.
(1)由题意得:![]() ,解得:
,解得:![]() .
.
答:图甲中a与b的值分别为:60、40.
(2)①由图示裁法一产生A型板材为:2×30=60,裁法二产生A型板材为:1×4=4,所以两种裁法共产生A型板材
为60+4=64(张),由图示裁法一产生B型板材为:1×30=30,裁法二产生A型板材为,2×4=8,所以两种裁法共产生B型板材
为30+8=38(张).
故答案为:64,38.
②由已知和图示得:横式无盖礼品盒的y个,每个礼品盒用2张B型板材,所以用B型板材2y张.
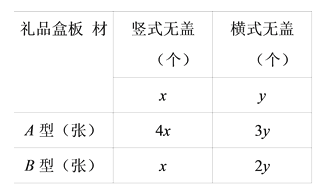
③由上表可知横式无盖款式共5y个面,用A型3y张,则B型需要2y张.
则做两款盒子共需要A型4x+3y张,B型x+2y张.
则4x+3y≤64;x+2y≤38.两式相加得5x+5y≤102.
则x+y≤20.4.所以最多做20个.
两式相减得3x+y≤26.则2x≤5.6,解得x≤2.8.则y≤18.
则横式可做16,17或18个.
故答案为:20,16或17或18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】联想三角形外心的概念,我们可引入如下概念. 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
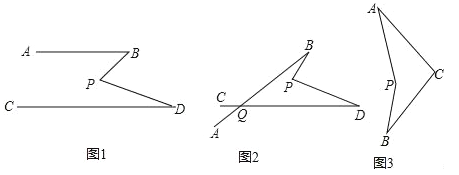
举例:如图1,若PA=PB,则点P为△ABC的准外心.
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= AB,求∠APB的度数.
AB,求∠APB的度数.
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,若AB∥CD,将点P在AB、CD内部,∠B,∠D,∠P满足的数量关系是 ,并说明理由.
(2)在图1中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图2,利用(1)中的结论(可以直接套用),求∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?
(3)科技活动课上,雨轩同学制作了一个图(3)的“飞旋镖”,经测量发现∠PAC=30°,∠PBC=35°,他很想知道∠APB与∠ACB的数量关系,你能告诉他吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真的探索.
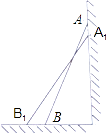
【思考题】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
(1)请你将小明对“思考题”的解答补充完整: 解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1=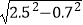 ﹣0.4=2
﹣0.4=2
而A1B1=2.5,在Rt△A1B1C中,由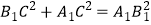 得方程 ,
得方程 ,
解方程得x1= , x2= ,
∴点B将向外移动米.
(2)解完“思考题”后,小聪提出了如下两个问题: 【问题一】在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
【问题二】在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S,若PR=PS,则下面三个结论:①AS=AR;②AQ=PQ;③△PQR≌△CPS;④AC﹣AQ=2SC,其中正确的是( )
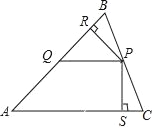
A. ②③④ B. ①② C. ①④ D. ①②③④
-
科目: 来源: 题型:
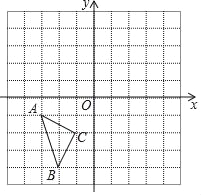
查看答案和解析>>【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)将△ABC关于x轴对称得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标;
(2)把△A1B1C1平移,使点B1平移到B2(3,4),请作出△A1B1C1平移后的△A2B2C2,并写出A2的坐标;
(3)已知△ABC中有一点D(a,b),求△A2B2C2中的对应点D2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
相关试题

