【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,交AC边于点E.过点D作⊙O的切线,交AC于点F,交AB的延长线于点G,连接DE. 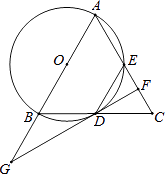
(1)求证:BD=CD;
(2)若∠G=40°,求∠AED的度数.
(3)若BG=6,CF=2,求⊙O的半径.
参考答案:
【答案】
(1)证明:连接AD,
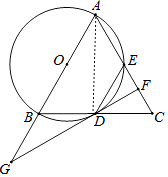
∵AB为直径,
∴∠ACB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD
(2)解:连接OD,
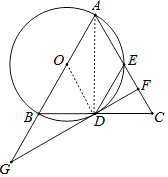
∵GF是切线,OD是半径,
∴OD⊥GF,
∴∠ODG=90°,
∵∠G=40°,
∴∠GOD=50°,
∵OB=OD,
∴∠OBD=65°,
∵点A、B、D、E都在⊙O上,
∴∠ABD+∠AED=180°,
∴∠AED=115°
(3)解:∵AB=AC,
∴∠ABC=∠C,
∵OB=OD,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴△GOD∽△GAF,
∴ ![]() =
= ![]() ,
,
∴设⊙O的半径是r,则AB=AC=2r,
∴AF=2r﹣2,
∴ ![]() =
= ![]() ,
,
∴r=3,
即⊙O的半径是3
【解析】(1)连接AD,根据圆周角定理得出AD⊥BC,根据等腰三角形的性质得出即可;(2)连接OD,根据切线的性质求出∠ODG=90°,求出∠BOD、∠ABC,根据圆内接四边形求出即可;(3)求出△ODG∽△AFG,得出比例式,即可求出圆的半径.
【考点精析】根据题目的已知条件,利用等腰三角形的性质和切线的性质定理的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=
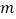 (
(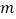 为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.(1)如图,当点C恰好在线段AB中点时,则PQ=_______(用含
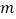 的代数式表示);
的代数式表示);(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ-2PQ与1的大小关系,并说明理由。
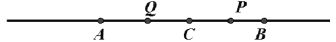
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD、DE、BE,则下列结论:①∠ECA=165°,②BE=BC;③AD=BE;④CD=BD.其中正确的是 ( )
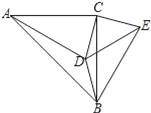
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:
计算代数式
 (其中x≠0)的值后填入下表.并根据表格所反映出的
(其中x≠0)的值后填入下表.并根据表格所反映出的 (其中x≠0)的值与x之间的变化规律进行探究.
(其中x≠0)的值与x之间的变化规律进行探究.x
……
0.25
0.5
1
10
100
1000
10000
……

……
……
下面是小东计算代数式
 (其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
(其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:x
……
0.25
0.5
1
10
100
1000
10000
……

……
2
1

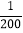
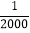
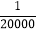
……
(1)上表是
 (其中x≠0)与x的几组对应值.直接写出x=10时,求代数式
(其中x≠0)与x的几组对应值.直接写出x=10时,求代数式 的值;
的值;(2)随着x值的增大,代数式
 的值有何变化(回答“增大”或“减少”);
的值有何变化(回答“增大”或“减少”);(3)当x值无限增大时,代数式
 的值无限趋近于一个数,这个数是多少.
的值无限趋近于一个数,这个数是多少. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=2x-4
(1)画出函数的图象;
(2)判断点A(1,-2),B(2,1)是否在该函数的图象上.
(3)已知点A(-2,b)在该函数图像上,求b值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点A(2,0)的两条直线
 ,
, 分别交
分别交 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB= .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求
 的解析式.
的解析式.
相关试题

