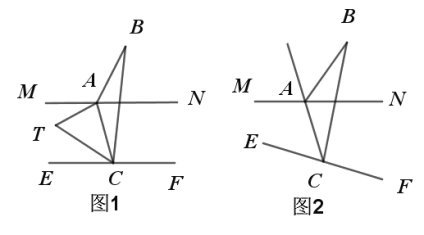
【题目】已知点A和点C分别在直线MN和直线EF上,点B在直线外,∠BAN=α,∠BCF=β.
(1)如图1,若MN∥EF,则∠B= (用α,β的式子表示,不写证明过程)
(2)在(1)的条件下,点T在直线MN与直线EF之间,∠MAT=![]() ∠BAN,∠TCB=2∠TCE,求∠B与∠T之间的数量关系.
∠BAN,∠TCB=2∠TCE,求∠B与∠T之间的数量关系.
(3)如图2,若MN不平行于EF,直线AC平分∠MAB,且平分∠ECB,则∠B= (用α,β的式子表示,不写证明过程)
参考答案:
【答案】(1)β-α;(2)∠ATC=-![]() ∠B+60°;(3)∠B=
∠B+60°;(3)∠B=![]() (β-α)
(β-α)
【解析】
(1)利用平行线的性质和三角形外角的性质求解即可;
(2)过T作TK∥MN,根据平行线的性质得出∠ATK=∠MAT,∠KTC=∠TCE,再由∠MAT=![]() ∠BAN,∠TCB=2∠TCE,表示出∠ATC=-
∠BAN,∠TCB=2∠TCE,表示出∠ATC=-![]() (β-α)+60°,结合∠B=β-α,即可求出结果;
(β-α)+60°,结合∠B=β-α,即可求出结果;
(3)根据题中条件可得:∠BAH=![]() (180°-α),∠BCA=
(180°-α),∠BCA=![]() (180°-β),结合∠BAH=∠B+∠BCA,可得∠B.
(180°-β),结合∠BAH=∠B+∠BCA,可得∠B.
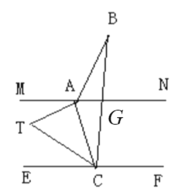
解:(1)如图,设MN与BC交于点G,
∵MN∥EF,
∴∠BGN=∠BCF=β,
∴∠B=∠BGN-∠BAN=β-α,
故答案为:β-α;
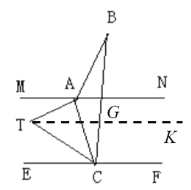
(2)如图,过T作TK∥MN,
∵MN∥EF,
∴∠ATK=∠MAT,∠KTC=∠TCE,
∵∠MAT=![]() ∠BAN,∠TCB=2∠TCE,
∠BAN,∠TCB=2∠TCE,
∴∠ATC=∠ATK+∠KTC
=∠MAT+∠TCE
=![]() ∠BAN+
∠BAN+![]() ∠TCB
∠TCB
=![]() α+
α+![]() ×
×![]() ×(180°-∠BCF)
×(180°-∠BCF)
=![]() α-
α-![]() β+60°
β+60°
=-![]() (β-α)+60°
(β-α)+60°
∵∠B=β-α,
∴∠ATC=-![]() ∠B+60°;
∠B+60°;
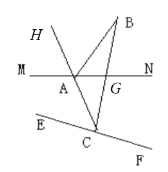
(3)如图,
∵直线AC平分∠MAB,且平分∠ECB,
∴∠BAH=∠MAH=![]() (180°-∠BAN)=
(180°-∠BAN)=![]() (180°-α),
(180°-α),
∠BCA=∠ECA=![]() (180°-∠BCF)=
(180°-∠BCF)=![]() (180°-β),
(180°-β),
∵∠BAH=∠B+∠BCA,
∴![]() (180°-α)=∠B+
(180°-α)=∠B+![]() (180°-β),
(180°-β),
∴∠B=![]() (β-α).
(β-α).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,AC∥BE,∠MAC=40,∠D=50°,CH平分∠ACD,BH平分∠ABD,
(1)求∠EBH的角度
(2)求∠BHC的角度

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小东设计的“作
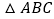 中
中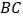 边上的高线”的尺规作图过程.
边上的高线”的尺规作图过程.已知:
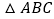 .
. 求作:
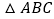 中
中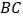 边上的高线
边上的高线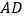 .
.作法:如图,
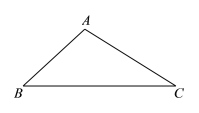
①以点
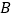 为圆心,
为圆心,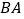 的长为半径作弧,以点
的长为半径作弧,以点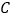 为圆心,
为圆心,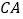 的长为半径作弧,两弧在
的长为半径作弧,两弧在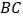 下方交于点
下方交于点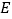 ;
;②连接
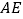 交
交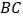 于点
于点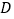 .
.所以线段
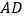 是
是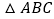 中
中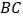 边上的高线.
边上的高线.根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵
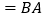 ,
, 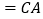 ,
,∴点
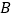 ,
,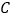 分别在线段
分别在线段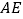 的垂直平分线上( )(填推理的依据).
的垂直平分线上( )(填推理的依据).∴
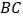 垂直平分线段
垂直平分线段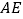 .
. ∴线段
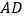 是
是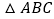 中
中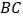 边上的高线.
边上的高线. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,5≤m<10时为B级,当0≤m<5为C级.现随机抽取30个符合年龄条件的青年人开展“每人日均发微博条数”的调查,所有抽青年人的“日均发微博条数”的数据如表:
11
10
6
15
9
16
13
12
0
8
2
8
10
17
6
13
7
5
7
3
12
10
7
11
3
6
8
14
15
12
(1)求样本数据中为A级的频率;
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取两人,用列举法求抽得两个人的“日均发微博条数”都是3的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列叙述不正确的是( )
A. 一个三角形必有三条中位线
B. 一个三角形必有三条中线
C. 三角形的一条中线分成的两个三角形的面积相等
D. 三角形的一条中位线分成的两部分面积相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF,CE.
求证:AF∥CE.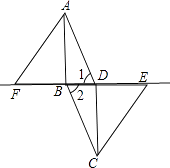
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
相关试题

