【题目】如图1,已知抛物线![]() 与y轴交于点A(0,﹣4),与x轴相交于B(﹣2,0)、C(4,0)两点,O为坐标原点.
与y轴交于点A(0,﹣4),与x轴相交于B(﹣2,0)、C(4,0)两点,O为坐标原点.
(1)求抛物线的解析式;
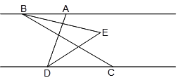
(2)设点E在x轴上,∠OEA+∠OAB=∠ACB,求BE的长;
(3)如图2,将抛物线y=ax2+bx+c向右平移n(n>0)个单位得到的新抛物线与x轴交于M、N(M在N左侧),P为x轴下方的新抛物线上任意一点,连PM、PN,过P作PQ⊥MN于Q,![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
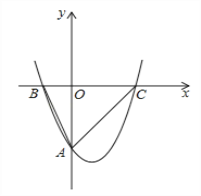
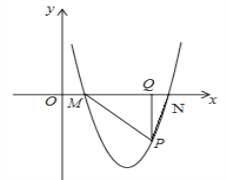
图1 图2
参考答案:
【答案】(1)y=![]() x2-x-4;(2)14或10;(3)是定值,理由见解析.
x2-x-4;(2)14或10;(3)是定值,理由见解析.
【解析】(1)由题意设抛物线解析式为y=a(x+2)(x-4),把(0,-4)代入求出a即可.
(2)由tan∠ACB=![]() =1,tan∠OAB=
=1,tan∠OAB=![]() =
=![]() ,可得tan∠OEA=
,可得tan∠OEA=![]() ,即
,即![]() =
=![]() ,从而根据正切函数的定义求出OE的值,进而可求BE的值;
,从而根据正切函数的定义求出OE的值,进而可求BE的值;
(3)设平移后的解析式为y=![]() (x+2-n)(x-4-n) ,点P的坐标为P(t,
(x+2-n)(x-4-n) ,点P的坐标为P(t,![]() (t+2-n)(t-4-n)),
(t+2-n)(t-4-n)),
表示出PQ、 MQ、NQ后,代入![]() +
+![]() 化简即可.
化简即可.
设(1)y=a(x+2)(x-4),将(0,-4)代入,得
-8a=-4a,
∴a=![]() ,
,
∴y=![]() (x+2)(x-4),即y=
(x+2)(x-4),即y=![]() x2-x-4;
x2-x-4;
(2). Rt△AOC中,tan∠ACB=![]() =1;
=1;
Rt△AOC中,tan∠OAB=![]() =
=![]() ,
,
∵∠OEA=∠ACB-∠OAB,
∴tan∠OEA=![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∵OA=4,
∴OE=12,
∴BE=12+2=14或BE=12-2=10,
答:BE的长为14或10;
(3)平移后:y=![]() (x+2-n)(x-4-n) ,
(x+2-n)(x-4-n) ,
∴ M(-2+n,0), N(4+n,0),
设P(t,![]() (t+2-n)(t-4-n)),
(t+2-n)(t-4-n)),
则PQ=-![]() (t+2-n)(t-4-n),
(t+2-n)(t-4-n),
MQ=t-(-2-n)=t+2-n, NQ=4+n-t,
∴![]() +
+![]() =
=![]() +
+![]() =-
=-![]() (t-4-n)+
(t-4-n)+![]() (t+2-n)=3为定值.
(t+2-n)=3为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“春节”是我国的传统佳节,民间历来有吃“汤圆”的习俗。某食品厂为了了解市民对去年销量较好的肉馅(A)、豆沙馅(B)、菜馅(C)、三丁馅(D)四种不同口味汤圆的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整)。请根据以上信息回答:
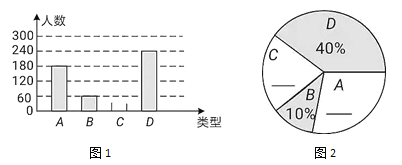
(1)从全体学生的调查表中随机抽取了多少名学生?
(2)将图1和图2补充完整;
(3)图2中表示“A”的圆心角是多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】从三角形一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.
(1)如图,在△ABC中,AD为角平分线,∠B=50°,∠C=30°,求证:AD为△ABC的优美线;
(2)在△ABC中,∠B=46°,AD是△ABC的优美线,且△ABD是以AB为腰的等腰三角形,求∠BAC的度数;
(3)在△ABC中,AB=4,AC=2,AD是△ABC的优美线,且△ABD是等腰三角形,直接写出优美线AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本,小亮用31元买了同样的钢笔2支和笔记本5本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作为奖品,奖给校运会表现突出的同学,要求笔记本数不少于钢笔数.请问:有多少购买方案?请你一一写出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=
 MF.其中正确结论的个数是( )
MF.其中正确结论的个数是( )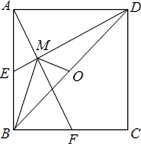
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△DCE有公共顶点C,AB=CD,BC=CE,∠ABC=∠DCE=90°.
(1)如图1,当点D在BC延长线上时.
①求证:△ABC≌△DCE.
②判断AC与DE的位置关系,并说明理由.
(2)如图2,△CDE从(1)中位置开始绕点C顺时针旋转,当点D落在BC边上时停止.
①若∠A=60°,记旋转的度数为
 ,当
,当 为何值时,DE与△ABC一边平行.
为何值时,DE与△ABC一边平行.②如图3,若AB=c, BC=a, AC=b, a>c,边BC,DE交于点F,求整个运动过程中,F在BC上的运动路程(用含a, b, c的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =68°.
(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
相关试题

