【题目】从三角形一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.
(1)如图,在△ABC中,AD为角平分线,∠B=50°,∠C=30°,求证:AD为△ABC的优美线;
(2)在△ABC中,∠B=46°,AD是△ABC的优美线,且△ABD是以AB为腰的等腰三角形,求∠BAC的度数;
(3)在△ABC中,AB=4,AC=2,AD是△ABC的优美线,且△ABD是等腰三角形,直接写出优美线AD的长.

参考答案:
【答案】(1)见解析;(2) 113°;(3) ![]() 或
或![]()
【解析】试题分析:(1)根据三角形的优美线的定义,只要证明△ABD是等腰三角形,
△CAD∽△CBA即可解决问题,(2)如图2中,分两种情形讨论求解①若AB=AD,
△CAD∽△CBA,则∠B=∠ADB=∠CAD,则AC∥BC,这与△ABC这个条件矛盾, ②若AB=BD, △CAD∽△CBA, (3)如图3中,分三种情形讨论①若AD=BD, △CAD∽△CBA,则![]() 设BD=AD=x,CD=y,可得
设BD=AD=x,CD=y,可得![]() ,解方程即可, ②若AB=AD=4,由
,解方程即可, ②若AB=AD=4,由![]() ,设BD=AD=x,CD=y,可得
,设BD=AD=x,CD=y,可得![]() ,解方程即可, ③若AB=AD,显然不可能.
,解方程即可, ③若AB=AD,显然不可能.
(1)证明:
∵∠B=50°,∠C=30°,∴∠BAC=100°,
∵AD平分∠BAC,
∴∠BAD=∠DAC=50°,
∴∠B=∠BAD=50°,∴DB=DA,
∴△ABD是等腰三角形,
∵∠C=∠C,∠DAC=∠B=50°,
∴△CAD∽△CBA,
∴线段AD是△ABC的优美线.
(2)若AB=AD,舍去,
(理由若△CAD∽△CBA,则∠B=∠ADB=∠CAD,则AC∥BC,)
若AB=BD,∠B=46°,
∴∠BAD=∠BDA=67°,
∵△CAD∽△CBA,
∴∠CAD=∠B=46°,
∴∠BAC=67°+46°=113°.
(3)![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△AOB中,∠AOB=90°,OA=OB=4厘米,点P从B出发,以1厘米/秒的速度沿边BO运动,设点P运动时间为x(x>0)秒.△APC是以AP为斜边的等腰直角三角形,且C,O两点在直线AB的同侧,连接OC.
(1)当x=1时,求
 的值;
的值;(2)当x=2时,求tan∠CAO的值;
(3)设△POC的面积为y,求y与x的函数解析式,并写出定义域.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,点D、E分别在边AB和AC上,DE∥BC,点F是DE延长线上的点,
 ,联结FC,
,联结FC,(1)求证:AB//CF;
(2)若
 ,FC=6,求AB的长.
,FC=6,求AB的长.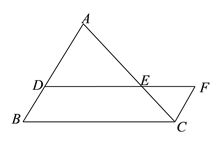
-
科目: 来源: 题型:
查看答案和解析>>【题目】a6可以表示为( )
A.a3a2
B.(a2)3
C.a12÷a2
D.a7﹣a -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题,其中真命题的个数是 ( )
①平行四边形的对边相等; ②;一条对角线平分一组对角的平行四边形是菱形.
③正方形既是轴对称图形,又是中心对称图形; ④对角线相等的四边形是矩形
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,( )是真命题.
A. 相等的角是对顶角B. 9的算术平方根是±3
C. 垂直于同一条直线的两条直线互相平行D. 点A(a,0)在x轴上
相关试题

