【题目】如图,△ABC与△DCE有公共顶点C,AB=CD,BC=CE,∠ABC=∠DCE=90°.
(1)如图1,当点D在BC延长线上时.
①求证:△ABC≌△DCE.
②判断AC与DE的位置关系,并说明理由.
(2)如图2,△CDE从(1)中位置开始绕点C顺时针旋转,当点D落在BC边上时停止.
①若∠A=60°,记旋转的度数为![]() ,当
,当![]() 为何值时,DE与△ABC一边平行.
为何值时,DE与△ABC一边平行.
②如图3,若AB=c, BC=a, AC=b, a>c,边BC,DE交于点F,求整个运动过程中,F在BC上的运动路程(用含a, b, c的代数式表示)

参考答案:
【答案】(1)①见解析;②AC⊥DE,理由见解析;(2)①60°或90°或150°
②![]()
【解析】
(1)①由边角边可证全等;
②延长AC与DE交于M,由△ABC≌△DCE得∠ACB=∠E,利用等角的余角相等可证结论.
(2)①根据题意,作出符合条件的三种情况,易得旋转角度.
②根据题意,作出F的最终位置,即可得出运动路径.
(1)①证明:在△ABC和△DCE中,

∴△ABC≌△DCE(SAS)
AC⊥DE,理由如下:
如图所示,延长AC与DE交于M,
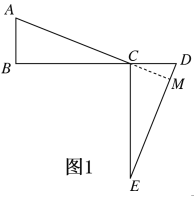
∵△ABC≌△DCE
∴∠ACB=∠E,
又∵∠ACB=∠DCM,∠E+∠D=90°
∴∠DCM+∠D=90°,
∴∠CMD=90°
即AC⊥DE.
(2)由题意可得,∠D=∠A=60°,∠E=∠ACB=30°,
(i)当DE∥BC时,如下图所示,
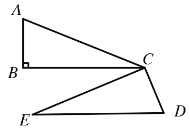
∵DE∥BC,
∴∠BCE=∠E=30°,
所以旋转角度![]() =90°-30°=60°
=90°-30°=60°
(ii)当DE∥AC时,如下图所示,此时BC和CE重合,

由图可知,![]() =∠BCD=90°
=∠BCD=90°
(iii)当DE∥AB时,如下图所示,
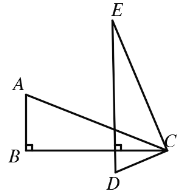
∵DE∥AB,AB⊥BC
∴DE⊥BC,
∴∠BCE=90°-30°=60°
∴![]() =90°+∠BCE=150°
=90°+∠BCE=150°
综上,![]() 为60°或90°或150°.
为60°或90°或150°.
②由题意可得,F点从B点开始运动到图1中![]() 点所示位置,然后再继续运动,返回到图2中F点重合,
点所示位置,然后再继续运动,返回到图2中F点重合,![]()
B点的运动路程为:![]()
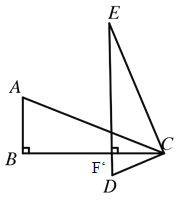

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本,小亮用31元买了同样的钢笔2支和笔记本5本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作为奖品,奖给校运会表现突出的同学,要求笔记本数不少于钢笔数.请问:有多少购买方案?请你一一写出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线
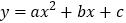 与y轴交于点A(0,﹣4),与x轴相交于B(﹣2,0)、C(4,0)两点,O为坐标原点.
与y轴交于点A(0,﹣4),与x轴相交于B(﹣2,0)、C(4,0)两点,O为坐标原点.(1)求抛物线的解析式;
(2)设点E在x轴上,∠OEA+∠OAB=∠ACB,求BE的长;
(3)如图2,将抛物线y=ax2+bx+c向右平移n(n>0)个单位得到的新抛物线与x轴交于M、N(M在N左侧),P为x轴下方的新抛物线上任意一点,连PM、PN,过P作PQ⊥MN于Q,
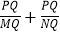 是否为定值?请说明理由.
是否为定值?请说明理由.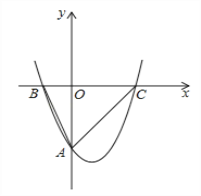
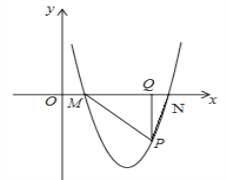
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=
 MF.其中正确结论的个数是( )
MF.其中正确结论的个数是( )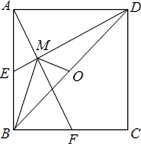
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =68°.
(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
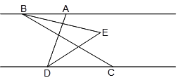
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是双曲线y=﹣
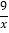 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=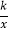 上运动,则k的值为_____.
上运动,则k的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填在上面各正方形中的四个数之间都有相同的规律,根据这种规律,
 的值应是__________.
的值应是__________.
相关试题

