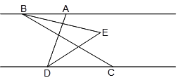
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =68°.
(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
参考答案:
【答案】(1)34°;(2)![]() n°+34°;(3)图形见解析;发生了改变, (214-
n°+34°;(3)图形见解析;发生了改变, (214-![]() n)°.
n)°.
【解析】
(1)根据角平分线的定义即可求∠EDC的度数;
(2)过点E作EF∥AB,然后根据两直线平行内错角相等,即可求∠BED的度数;
(3)∠BED的度数改变.过点E作EF∥AB,先由角平分线的定义可得:
![]()
![]() ,然后根据两直线平行内错角相等及同旁内角互补可得:
,然后根据两直线平行内错角相等及同旁内角互补可得:![]() 进而可求
进而可求![]()
解:(1)∵DE平分∠ADC,∠ADC=68°,
∴![]()
(2)过点E作EF∥AB,
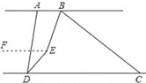
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=68°,
∴![]()
∴![]()
(3)过点E作EF∥AB
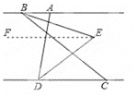
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=68°
∴![]()
∵AB∥CD,
∴AB∥CD∥EF,
∴![]()
∴![]()
故∠BED的度数发生了改变,改变为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线
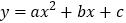 与y轴交于点A(0,﹣4),与x轴相交于B(﹣2,0)、C(4,0)两点,O为坐标原点.
与y轴交于点A(0,﹣4),与x轴相交于B(﹣2,0)、C(4,0)两点,O为坐标原点.(1)求抛物线的解析式;
(2)设点E在x轴上,∠OEA+∠OAB=∠ACB,求BE的长;
(3)如图2,将抛物线y=ax2+bx+c向右平移n(n>0)个单位得到的新抛物线与x轴交于M、N(M在N左侧),P为x轴下方的新抛物线上任意一点,连PM、PN,过P作PQ⊥MN于Q,
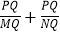 是否为定值?请说明理由.
是否为定值?请说明理由.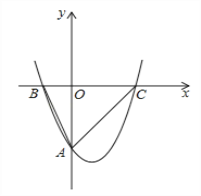
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=
 MF.其中正确结论的个数是( )
MF.其中正确结论的个数是( )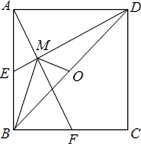
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△DCE有公共顶点C,AB=CD,BC=CE,∠ABC=∠DCE=90°.
(1)如图1,当点D在BC延长线上时.
①求证:△ABC≌△DCE.
②判断AC与DE的位置关系,并说明理由.
(2)如图2,△CDE从(1)中位置开始绕点C顺时针旋转,当点D落在BC边上时停止.
①若∠A=60°,记旋转的度数为
 ,当
,当 为何值时,DE与△ABC一边平行.
为何值时,DE与△ABC一边平行.②如图3,若AB=c, BC=a, AC=b, a>c,边BC,DE交于点F,求整个运动过程中,F在BC上的运动路程(用含a, b, c的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是双曲线y=﹣
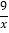 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=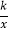 上运动,则k的值为_____.
上运动,则k的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填在上面各正方形中的四个数之间都有相同的规律,根据这种规律,
 的值应是__________.
的值应是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年假期某校对操场进行了维修改造,如图是操场的一角.在长为
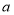 米,宽为
米,宽为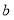 米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为
米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为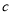 米.
米.(1)直接写出一个篮球场的长和宽;(用含字母
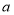 ,
,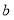 ,
,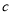 的代数式表示)
的代数式表示)(2)用含字母
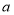 ,
,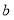 ,
,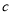 的代数式表示这两个篮球场占地面积的和,并求出当
的代数式表示这两个篮球场占地面积的和,并求出当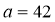 ,
,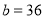 ,
, 时,这两个篮球场占地面积的和.
时,这两个篮球场占地面积的和.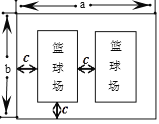
相关试题

