【题目】已知抛物线y=x2+(2m+1)x+m(m﹣3)(m为常数,﹣1≤m≤4).A(﹣m﹣1,y1),B( ![]() ,y2),C(﹣m,y3)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
,y2),C(﹣m,y3)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
(1)用含m的代数式表示抛物线的顶点坐标;
(2)若无论m取何值,抛物线与直线y=x﹣km(k为常数)有且仅有一个公共点,求k的值;
(3)当1<PH≤6时,试比较y1 , y2 , y3之间的大小.
参考答案:
【答案】
(1)
解:∵﹣ ![]() =﹣
=﹣ ![]() ,
, ![]() =
= ![]() =﹣
=﹣ ![]() ,
,
∴顶点坐标(﹣ ![]() ,﹣
,﹣ ![]() )
)
(2)
解:由 ![]() 消去y得x2+2mx+(m2+km﹣3m)=0,
消去y得x2+2mx+(m2+km﹣3m)=0,
∵抛物线与x轴有且仅有一个公共点,
∴△=0,即(k﹣3)m=0,
∵无论m取何值,方程总是成立,
∴k﹣3=0,
∴k=3
(3)
解:PH=|﹣ ![]() ﹣(﹣
﹣(﹣ ![]() )|=|
)|=| ![]() |,
|,
∵1<PH≤6,
∴当 ![]() >0时,有1<
>0时,有1< ![]() ≤6,又﹣1≤m≤4,
≤6,又﹣1≤m≤4,
∴ ![]() <m≤
<m≤ ![]() ,
,
当 ![]() <0时,1<﹣
<0时,1<﹣ ![]() ≤6,又∵﹣1≤m≤4,
≤6,又∵﹣1≤m≤4,
∴ ![]() ,
,
∴﹣1≤m<﹣ ![]() 或
或 ![]() <m≤
<m≤ ![]() ,
,
∵A(﹣m﹣1,y1)在抛物线上,
∴y1=(﹣m﹣1)2+(2m+1)(﹣m﹣1)+m(m+3)=﹣4m,
∵C(﹣m,y3)在抛物线上,
∴y3=(﹣m)2+(2m+1)(﹣m)+m(m﹣3)=﹣4m,
∴y1=y3,
①令 ![]() <﹣m﹣1,则有m<﹣
<﹣m﹣1,则有m<﹣ ![]() ,结合﹣1≤m≤﹣
,结合﹣1≤m≤﹣ ![]() ,
,
∴﹣1≤m<﹣ ![]() ,
,
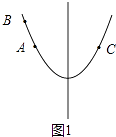
此时,在对称轴的左侧y随x的增大而减小,如图1:
 ,
,
∴y2>y1=y3,
即当﹣1≤m<﹣ ![]() 时,有y2>y1=y3.
时,有y2>y1=y3.
②令 ![]() =﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
=﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
③令 ![]() >﹣m﹣1,且
>﹣m﹣1,且 ![]() ≤﹣
≤﹣ ![]() 时,有﹣
时,有﹣ ![]() <m≤﹣
<m≤﹣ ![]() ,结合﹣1≤m<﹣
,结合﹣1≤m<﹣ ![]() ,
,
∴﹣ ![]() <m≤﹣
<m≤﹣ ![]() ,
,
此时,在对称轴的左侧,y随x的增大而减小,如图2:

∴y1=y3>y2,
即当﹣ ![]() <m≤﹣
<m≤﹣ ![]() 时,有y1=y3>y2,
时,有y1=y3>y2,
④令﹣ ![]() ≤
≤ ![]() <﹣m,有﹣
<﹣m,有﹣ ![]() ≤m<0,结合﹣1≤m<﹣
≤m<0,结合﹣1≤m<﹣ ![]() ,
,
∴﹣ ![]() ≤m<﹣
≤m<﹣ ![]() ,
,
此时,在对称轴的右侧y随x的增大而增大,如图3:

∴y2<y3=y1.
⑤令 ![]() =﹣m,B,C重合,不合题意舍弃.
=﹣m,B,C重合,不合题意舍弃.
⑥令 ![]() >﹣m,有m>0,结合
>﹣m,有m>0,结合 ![]() <m≤
<m≤ ![]() ,
,
∴ ![]() <m≤
<m≤ ![]() ,
,
此时,在对称轴的右侧,y随x的增大而增大,如图4:
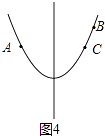
∴y2>y3=y1,
即当 ![]() <m≤
<m≤ ![]() 时,有y2>y3=y1,
时,有y2>y3=y1,
综上所述,﹣1≤m<﹣ ![]() 或
或 ![]() <m≤
<m≤ ![]() 时,有y2>y1=y3,
时,有y2>y1=y3,
﹣ ![]() <m<﹣
<m<﹣ ![]() 时,有y2<y1=y3.
时,有y2<y1=y3.
【解析】(1)根据顶点坐标公式即可解决问题.(2)列方程组根据△=0解决问题.(3)首先证明y1=y3 , 再根据点B的位置,分类讨论,①令 ![]() <﹣m﹣1,求出m的范围即可判断,②令
<﹣m﹣1,求出m的范围即可判断,②令 ![]() =﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
=﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
③令 ![]() >﹣m﹣1,求出m的范围即可判断,④令﹣
>﹣m﹣1,求出m的范围即可判断,④令﹣ ![]() ≤
≤ ![]() <﹣m,求出m的范围即可判断,⑤令
<﹣m,求出m的范围即可判断,⑤令 ![]() =﹣m,B,C重合,不合题意舍弃.⑥令
=﹣m,B,C重合,不合题意舍弃.⑥令 ![]() >﹣m,求出m的范围即可判断.本题考查二次函数综合题、顶点坐标公式等知识,解题的关键是熟练掌握利用根的判别式解决抛物线与直线的交点问题,学会分类讨论,学会利用函数图象判断函数值的大小,属于中考压轴题.
>﹣m,求出m的范围即可判断.本题考查二次函数综合题、顶点坐标公式等知识,解题的关键是熟练掌握利用根的判别式解决抛物线与直线的交点问题,学会分类讨论,学会利用函数图象判断函数值的大小,属于中考压轴题.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E.

(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1, =1.4,
=1.4, 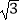 =1.7)
=1.7) -
科目: 来源: 题型:
查看答案和解析>>【题目】某蛋糕产销公司A品牌产销线,2015年的销售量为9.5万份,平均每份获利1.9元,预计以后四年每年销售量按5000份递减,平均每份获利按一定百分数逐年递减;受供给侧改革的启发,公司早在2104年底就投入资金10.89万元,新增一条B品牌产销线,以满足市场对蛋糕的多元需求,B品牌产销线2015年的销售量为1.8万份,平均每份获利3元,预计以后四年销售量按相同的份数递增,且平均每份获利按上述递减百分数的2倍逐年递增;这样,2016年,A、B两品牌产销线销售量总和将达到11.4万份,B品牌产销线2017年销售获利恰好等于当初的投入资金数.
(1)求A品牌产销线2018年的销售量;
(2)求B品牌产销线2016年平均每份获利增长的百分数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=6,AC=8,BC=10,D是△ABC内部或BC边上的一个动点(与B、C不重合),以D为顶点作△DEF,使△DEF∽△ABC(相似比k>1),EF∥BC.

(1)求∠D的度数;
(2)若两三角形重叠部分的形状始终是四边形AGDH.
①如图1,连接GH、AD,当GH⊥AD时,请判断四边形AGDH的形状,并证明;
②当四边形AGDH的面积最大时,过A作AP⊥EF于P,且AP=AD,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
 的解集表示在数轴上,正确的是( )
的解集表示在数轴上,正确的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )

A.1:3
B.1:4
C.1:5
D.1:25 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某工件的三视图,则此工件的表面积为( )

A.15πcm2
B.51πcm2
C.66πcm2
D.24πcm2
相关试题

