【题目】如图,图中的小方格都是边长为1的正方形,△ABC的A,B,C三点坐标为A(2,0)、B(2,2)、C(6,3)。
(1)请在图中画出一个△ ![]() ,使△
,使△ ![]() 与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
(2)求△ ![]() 的面积。
的面积。
参考答案:
【答案】
(1)解:∵A(2,0)、B(2,2)、C(6,3),△A′B′C′与△ABC是以坐标原点为位似中心,相似比为2的位似图形,
∴A′(4,0),B′(4,4),C′(12,6),如图:
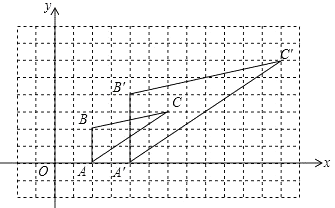
(2)解:S△A′B′C′= ![]() ×4×8=16
×4×8=16
【解析】(1)分别连接OB、OA,并延长至B',A',C',使OB'=2OB,OA'=2OA,OC'=2OC,顺次连接A'、B'、C';(2)利用面积公式即可算出.
【考点精析】解答此题的关键在于理解位似变换的相关知识,掌握它们具有相似图形的性质外还有图形的位置关系(每组对应点所在的直线都经过同一个点—位似中心),以及对作图-位似变换的理解,了解对应点到位似中心的距离比就是位似比,对应线段的比等于位似比,位似比也有顺序;已知图形的位似图形有两个,在位似中心的两侧各有一个.位似中心,位似比是它的两要素.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,∠B=30°,AB≠BC ,将△ABC沿AC翻折至△AB′C ,连结B ′D. 若
 ,∠AB ′D=75°,则BC= .
,∠AB ′D=75°,则BC= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP=
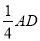 ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了二次根式的相关运算后,我们发现一些含有根号的式子可以表示成另一个式子的平方,如:
3+2
 =2+2
=2+2 +1=(
+1=( )2+2
)2+2 +1=(
+1=( +1)2;
+1)2;5+2
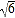 =2+2
=2+2 +3=(
+3=( )2+2×
)2+2× ×
× +(
+( )2=(
)2=( +
+ )2
)2(1)请仿照上面式子的变化过程,把下列各式化成另一个式子的平方的形式:
①4+2
 ;②6+4
;②6+4
(2)若a+4
 =(m+n
=(m+n )2,且a,m,n都是正整数,试求a的值.
)2,且a,m,n都是正整数,试求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(B,F,D在同一条直线上)。一直小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:
 ≈1.732,
≈1.732,  ≈1.414,结果保留整数)
≈1.414,结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下面解方程组的方法,然后解决有关问题:解方程组
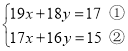 时,如果直接消元,那将会很繁琐,若采用下面的解法,则会简单很多.
时,如果直接消元,那将会很繁琐,若采用下面的解法,则会简单很多.解:①-②,得:2x+2y=2,即x+y=1③
③×16,得:16x+16y=16④
②-④,得:x=-1
将x=-1
代入③得:y=2
∴原方程组的解为:

(1)请你采用上述方法解方程组:

(2)请你采用上述方法解关于x,y的方程组
 ,其中
,其中 .
.
相关试题

