【题目】已知:把Rt△ABC和Rt△DEF按如图1摆放(点C与点E重合),点B、C(E)、F在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm,如图2,△DEF从图1的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
(1)用含t的代数式表示线段AP= ;
(2)当t为何值时,点E在∠A的平分线上?
(3)当t为何值时,点A在线段PQ的垂直平分线上?
(4)连接PE,当t=1(s)时,求四边形APEC的面积.

参考答案:
【答案】(1)(10﹣2t)cm.(2)![]() ;(3)t=2;(4)20
;(3)t=2;(4)20
【解析】
(1)利用勾股定理求出AB,根据AP=AB﹣BP计算即可.
(2)如图1中,作AT平分∠BAC,作TH⊥AB于H.设TC=TH=x,证明Rt△ATH≌Rt△ATC(HL),推出AH=AC=8,在Rt△BTH中,则有(6﹣x)2=22+x2,求出x即可解决问题.
(3)根据线段垂直平分线的性质得到AP=AQ,根据等腰三角形的性质得到CE=CQ,根据勾股定理求出AB,列式计算即可.
(4)作PM⊥BE交BE于M,根据S四边形APEC=S△ABC﹣S△BPE计算算即可.
(1)在Rt△ABC中,∵∠ACB=90°,AC=8cm,BC=6cm,
∴AB=![]() =
=![]() =10(cm),
=10(cm),
由题意PA=AB﹣BP=(10﹣2t)cm,
故答案为(10﹣2t)cm.
(2)如图1中,作AT平分∠BAC,作TH⊥AB于H.
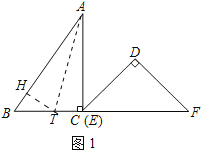
∵TC⊥AC,TH⊥AB,TA平分∠ABC,
∴TC=TH,∠AHT=∠ACT=90°,设TC=TH=x,
∵AT=AT,
∴Rt△ATH≌Rt△ATC(HL),
∴AH=AC=8,
∴BH=AB﹣AH=10﹣8=2,
在Rt△BTH中,则有(6﹣x)2=22+x2,
解得x=![]() ,
,
∴当t为![]() 时,点E在∠A的平分线上.
时,点E在∠A的平分线上.
(3)∵点A在线段PQ的垂直平分线上,
∴AP=AQ,
∵∠DEF=45°,∠ACB=90°,∠DEF+∠ACB+∠EQC=180°,
∴∠EQC=45°,
∴∠DEF=∠EQC,
∴CE=CQ,
由题意知:CE=t,BP=2t,
∴CQ=t,
∴AQ=8﹣t,
在Rt△ABC中,由勾股定理得,AB=10cm,
则AP=10﹣2t,
∴10﹣2t=8﹣t,
解得:t=2,
答:当t=2s时,点A在线段PQ的垂直平分线上;
(4)如图2中,过P作PM⊥BE,交BE于M,
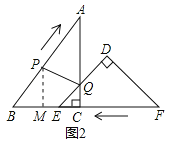
∴∠BMP=90°,
在Rt△ABC和Rt△BPM中,sinB=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得,PM=![]() ,
,
∵BC=6cm,CE=t,
∴BE=6﹣1=5,
∴S四边形APEC=S△ABC﹣S△BPE=![]() ×BC×AC﹣
×BC×AC﹣![]() ×BE×PM=
×BE×PM=![]() ×6×8﹣
×6×8﹣![]() ×5×
×5×![]() =20.
=20.
-
科目: 来源: 题型:
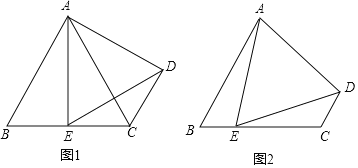
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,AB=BC,∠B=60°,E是BC边上一点.
(1)如图1,若E是BC的中点,∠AED=60°,求证:CE=CD;
(2)如图2,若∠EAD=60°,求证:△AED是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数的图象的对称轴是直线
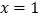 ,它与
,它与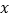 轴交于
轴交于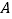 、
、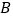 两点,与
两点,与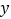 轴交与点
轴交与点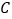 ,点
,点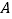 、
、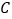 的坐标分别是
的坐标分别是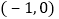 、
、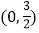 .
.
(1)请在平面直角坐标系内画出示意图;
(2)求此图象所对应的函数关系式;
(3)若点
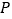 是此二次函数图象上位于
是此二次函数图象上位于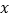 轴上方的一个动点,求
轴上方的一个动点,求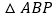 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
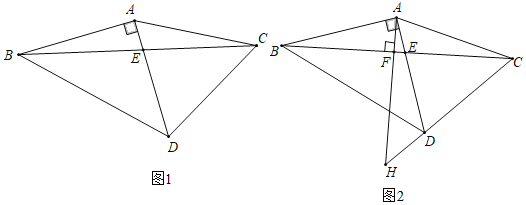
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,以AB为直角边作等腰直角三角形ABD,与BC边交于点E,
(1)若∠ACE=18°,则∠ECD=
(2)探索:∠ACE与∠ACD有怎样的数量关系?猜想并证明.
(3)如图2,作△ABC的高AF并延长,交BD于点G,交CD延长线于点H,求证:CH2+DH2=2AD2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
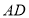 是
是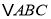 的角平分线,
的角平分线,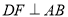 ,垂足为
,垂足为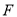 ,
,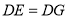 ,
,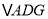 和
和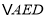 的面积分别为49,40,则
的面积分别为49,40,则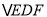 的面积为( )
的面积为( )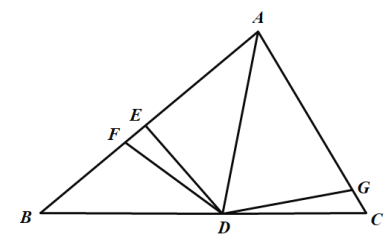
A.3.5B.4.5C.9D.10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
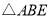 ,
,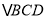 均为等边三角形,点
均为等边三角形,点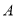 ,
,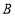 ,
,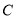 在同一条直线上,连接
在同一条直线上,连接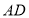 ,
,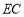 ,
,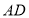 与
与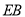 相交于点
相交于点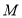 ,
,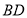 与
与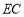 相交于点
相交于点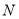 ,连接
,连接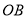 ,下列结论正确的有_________.
,下列结论正确的有_________.①
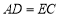 ;②
;②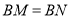 ;③
;③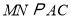 ;④
;④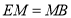 ;⑤
;⑤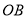 平分
平分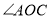
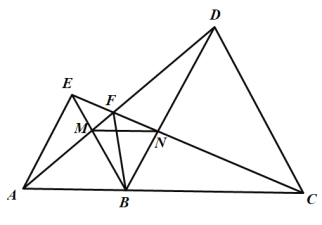
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
(3)点P(a+1,b-1)与点C关于x轴对称,则a= ,b= .

相关试题

