【题目】如图,![]() ,
,![]() 均为等边三角形,点
均为等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上,连接
在同一条直线上,连接![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,下列结论正确的有_________.
,下列结论正确的有_________.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 平分
平分![]()
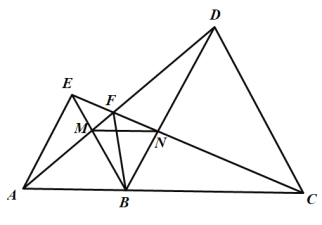
参考答案:
【答案】①②③⑤.
【解析】
由题意根据全等三角形的判定和性质以及等边三角形的性质和角平分线的性质,对题干结论依次进行分析即可.
解:∵△ABE,△BCD均为等边三角形,
∴AB=BE,BC=BD,∠ABE=∠CBD=60°,
∴∠ABD=∠EBC,
在△ABD和△EBC中,
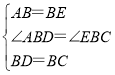
∴△ABD≌△EBC(SAS),
∴AD=EC,故①正确;
∴∠DAB=∠BEC,
又由上可知∠ABE=∠CBD=60°,
∴∠EBD=60°,
在△ABM和△EBN中,
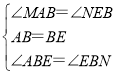
∴△ABM≌△EBN(ASA),
∴BM=BN,故②正确;
∴△BMN为等边三角形,
∴∠NMB=∠ABM=60°,
∴MN∥AC,故③正确;
若EM=MB,则AM平分∠EAB,
则∠DAB=30°,而由条件无法得出这一条件,
故④不正确;
如图作![]()
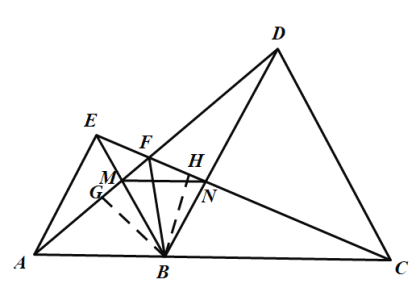
∵由上可知△ABD≌△EBC,
∴两个三角形对应边的高相等即![]() ,
,
∴![]() 是
是![]() 的角平分线,即有
的角平分线,即有![]() 平分
平分![]() ,故⑤正确.
,故⑤正确.
综上可知:①②③⑤正确.
故答案为:①②③⑤.
-
科目: 来源: 题型:
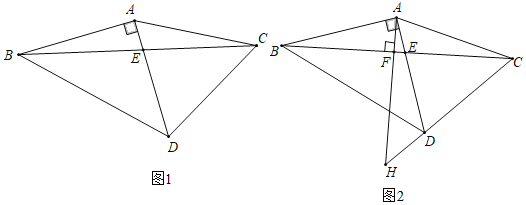
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,以AB为直角边作等腰直角三角形ABD,与BC边交于点E,
(1)若∠ACE=18°,则∠ECD=
(2)探索:∠ACE与∠ACD有怎样的数量关系?猜想并证明.
(3)如图2,作△ABC的高AF并延长,交BD于点G,交CD延长线于点H,求证:CH2+DH2=2AD2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:把Rt△ABC和Rt△DEF按如图1摆放(点C与点E重合),点B、C(E)、F在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm,如图2,△DEF从图1的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
(1)用含t的代数式表示线段AP= ;
(2)当t为何值时,点E在∠A的平分线上?
(3)当t为何值时,点A在线段PQ的垂直平分线上?
(4)连接PE,当t=1(s)时,求四边形APEC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
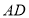 是
是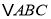 的角平分线,
的角平分线,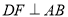 ,垂足为
,垂足为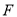 ,
,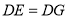 ,
,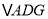 和
和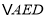 的面积分别为49,40,则
的面积分别为49,40,则 的面积为( )
的面积为( )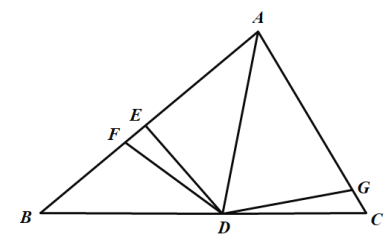
A.3.5B.4.5C.9D.10
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
(3)点P(a+1,b-1)与点C关于x轴对称,则a= ,b= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
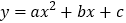 的图象开口向上,图象经过点
的图象开口向上,图象经过点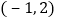 和
和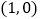 ,且与
,且与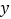 轴相交于负半轴.
轴相交于负半轴.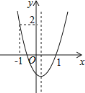
第
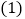 问:给出四个结论:①
问:给出四个结论:① ;②
;② ;③
;③ ;④
;④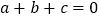 .写出其中正确结论的序号(答对得
.写出其中正确结论的序号(答对得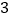 分,少选、错选均不得分)
分,少选、错选均不得分)第
 问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号.
问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的顶点A、B的坐标分别为(-4,0)和(2,0),BC=
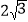 .设直线AC与直线x=4交于点E.
.设直线AC与直线x=4交于点E.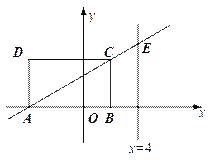
(1)求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E;
(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于C、N之间的一动点,求△CMN面积的最大值.
相关试题

