Question

【题目】如图，AD∥BC，AF平分∠BAD交BC于点F，BE平分∠ABC交AD于点E．求证：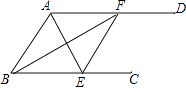

（1）△ABF是等腰三角形；
（2）四边形ABFE是菱形．

Answer 1

【答案】
（1）证明：∵AD∥BC，

∴∠AFB=∠EBF，

∵BF平分∠ABC，

∴∠ABF=∠EBF，

∴∠AFB=∠ABF，

∴AB=AF，即△ABF是等腰三角形

（2）证明：由（1）得：AB=AF，

同理：AB=BE，

∴AF=BE，

∵AF∥BE，

∴四边形ABFE是平行四边形，

又∵AB=AF，

∴四边形ABFE是菱形

【解析】（1）由平行线的性质和角平分线得出∠AFB=∠ABF，即可得出结论；（2）由（1）得：AB=AF，同理：AB=BE，证出AF=BE，由AF∥BE，得出四边形ABFE是平行四边形，即可得出结论．
【考点精析】本题主要考查了等腰三角形的判定和菱形的判定方法的相关知识点，需要掌握如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等；任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形才能正确解答此题．