【题目】某商场一种商品的进价为每件30元,售价为每件40元,每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若该商品每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?
(3)在(2)的条件下,每件商品的售价为多少元时,每天可获得最大利润?最大利润是多少元?
参考答案:
【答案】
(1)解:设每次降价的百分率为x.
40×(1﹣x)2=32.4,
解得x=10%或190%(190%不符合题意,舍去).
答:该商品连续两次下调相同的百分率后售价降至每件32.4元,两次下降的百分率为10%
(2)解:设每天要想获得510元的利润,且更有利于减少库存,则每件商品应降价y元,由题意,得
(40﹣30﹣y)(4× ![]() +48)=510,
+48)=510,
解得:y1=1.5,y2=2.5,
∵有利于减少库存,
∴y=2.5.
答:要使商场每月销售这种商品的利润达到510元,且更有利于减少库存,则每件商品应降价2.5元
(3)解:设每件商品应降价y元,获得利润为W,
由题意得,W=(40﹣30﹣y)(4× ![]() +48)=﹣8y2+32y+480=﹣8(y﹣2)2+512,
+48)=﹣8y2+32y+480=﹣8(y﹣2)2+512,
故每件商品的售价为38元时,每天可获得最大利润,最大利润是512元
【解析】(1)设每次降价的百分率为x,(1﹣x)2为两次降价的百分率,40降至32.4就是方程的平衡条件,列出方程求解即可;(2)设每天要想获得510元的利润,且更有利于减少库存,则每件商品应降价y元,由销售问题的数量关系建立方程求出其解即可;(3)设每件商品应降价y元,获得利润为W,根据题意得到函数解析式,即可得到最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.

(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=10,EF=6,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证:
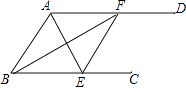
(1)△ABF是等腰三角形;
(2)四边形ABFE是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题.
大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,但是由于1<
的小数部分我们不可能全部地写出来,但是由于1< <2,所以
<2,所以 的整数部分为1,将
的整数部分为1,将 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分 -1,根据以上的内容,解答下面的问题:
-1,根据以上的内容,解答下面的问题:(1)
 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;(2)1+
 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;(3)若设2+
 整数部分是x,小数部分是y,求x-y的值.
整数部分是x,小数部分是y,求x-y的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地区5000名九年级学生体育成绩状况,随机抽取了若干名学生进行测试,将成绩按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
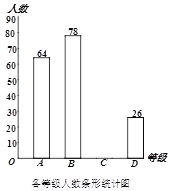
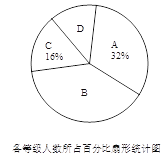
(1)在这次抽样调查中,一共抽取了______名学生;
(2)请把条形统计图补充完整;
(3)请估计该地区九年级学生体育成绩为B级的人数.
相关试题

