【题目】已知关于x的方程mx2﹣(3m﹣1)x+2m﹣2=0
(1)求证:无论m取任何实数时,方程恒有实数根;
(2)若关于x的二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2,且抛物线的开口向上时,求此抛物线的解析式;
(3)在坐标系中画出(2)中的函数图象,分析当直线y=x+b与(2)中的图象只有两个交点时b的取值范围.
参考答案:
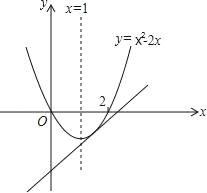
【答案】(1)见解析; (2)所求抛物线的解析式为:y=x2﹣2x;(3)当b>﹣![]() 时,直线y=x+b与(2)中的图象只有两个交点.
时,直线y=x+b与(2)中的图象只有两个交点.
【解析】试题分析:(1)二次项系数m的值不确定,分为m=0,m≠0两种情况,分别证明方程有实数根;
(2)设抛物线与x轴两交点的横坐标为x1,x2,则两交点之间距离为|x1-x2|=2,再与根与系数关系的等式结合变形,可求m的值,从而确定抛物线的解析式;
(3)联立方程组,有解时,求出b的取值范围.
试题解析:
(1)分两种情况讨论.
①当m=0时,方程为x﹣2=0,x=2.
∴m=0时,方程有实数根.
②当m≠0时,则一元二次方程的根的判别式
△=[﹣(3m﹣1)]2﹣4m(2m﹣2)
=9m2﹣6m+1﹣8m2+8m=m2+2m+1
=(m+1)2≥0,
∴m≠0时,方程有实数根.
故无论m取任何实数时,方程恒有实数根.
综合①②可知,m取任何实数,方程mx2﹣(3m﹣1)x+2m﹣2=0恒有实数根;
(2)设x1,x2为抛物线y=mx2﹣(3m﹣1)x+2m﹣2与x轴交点的横坐标.
则有x1+x2=![]() ,x1x2=
,x1x2=![]()
由|x1﹣x2|=![]() =|
=|![]() |,
|,
由|x1﹣x2|=2得|![]() |=2,
|=2,
∴![]() =2或
=2或![]() =﹣2
=﹣2
∴m=1或m=﹣![]()
而抛物线开口向上,
∴m=1
∴所求抛物线的解析式为:y=x2﹣2x;
(3)在(2)的条件下,直线y=x+b与抛物线y1,y2组成的图象只有两个交点,
联立得, ![]() ,
,
∴x2﹣3x﹣b=0,
∴△=9+4b>0,解得b>﹣![]() ;
;
当b>﹣![]() 时,直线y=x+b与(2)中的图象只有两个交点.
时,直线y=x+b与(2)中的图象只有两个交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
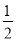 x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下面给出的数轴,解答下面的问题:
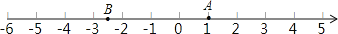
(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: ,B: ;
(2)观察数轴,与点A的距离为4的点表示的数是: ;
(3)若将数轴折叠,使得A点与﹣3表示的点重合,则B点与数 表示的点重合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在实施城乡清洁工作过程中,某校对各个班级教室卫生情况的考评包括以下几项:黑板、门窗、桌椅、地面.一天,两个班级的各项卫生成绩分别如下表:(单位:分)

黑板
门窗
桌椅
地面
一班
95
85
89
91
二班
90
95
85
90
(1)两个班的平均得分分别是多少?
(2)按学校的考评要求,将黑板、门窗、桌椅、地面这四项得分依次按15%、10%、35%、40%的权重计算各班的卫生成绩,那么哪个班的卫生成绩较高?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若矩形的一条角平分线分一边为3cm和5cm两部分,则矩形的周长为( )
A.22B.26C.22或26D.28或26
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的中点,P是线段BD上的一个动点,则PM+PN的最小值是( )
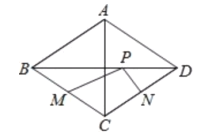
A.
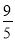 B.3
B.3C.
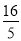 D.5
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如:
|6+7|=6+7;|6-7|=7-6;|7-6|=7-6;|-6-7|=6+7;
根据上面的规律,把下列各式写成去掉绝对值符号的形式:
(1)|7-21|=_________;
(2)|-
 +0.8|=____________;
+0.8|=____________;(3)|
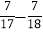 |=__________;
|=__________;(4)用合理的方法计算:|
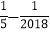 |+|
|+|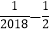 |-|-
|-|- |-
|- ×|-
×|- |+
|+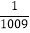 .
.
相关试题

