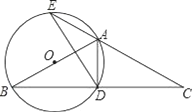
【题目】如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
(1)求证:D是BC的中点;
(2)若DE=3,BD﹣AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
参考答案:
【答案】(1)证明详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据直径所对的圆周角是直角得到AD⊥BC,应用等腰三角形的三线合一证得点D为BC的中点;
(2)应用等腰三角形的性质和判定证得BD=DE=3,进而求得BD=3,AD=1,应用勾股定理求得AB的长,即可得到半径的长;
(3)解法一:通过证明△CAB∽△CDE,应用相似三角形的性质解得CE的长,再求AE的长;
解法二:连接BE,通过证明△ADC∽△BEC,解得CE的长,再求AE的长.
试题解析:(1)证明:∵AB为⊙O的直径,
∴AD⊥BC,
又∵AB=AC,
∴D是BC的中点.
(2)解:∵AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠C=∠E,则DC=DE,
∴BD=DE=3,
又BD-AD=2,
∴AD=1,
在Rt△ABD中,BD=3,AD=1,
∴AB=![]() ,
,
则⊙O的半径为![]() .
.
(3)解法一:在△CAB和△CDE中,
∠B=∠E,∠C=∠C(公共角),
∴△CAB∽△CDE,
∴![]() ,
,
∵CA=AB=![]() ,
,
∴![]() ,
,
∴AE=CE-AC=![]() =
=![]() .
.
解法二:连接BE,
∵AB为⊙O的直径,
∴∠BEC=![]() ,
,
在△ADC和△BEC中,
∠ADC=∠BEC=![]() ,∠C=∠C,
,∠C=∠C,
∴△ADC∽△BEC,
∴![]() ,
,
∴![]() ,
,
∴AE=CE-AC=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
证明:(1)CF=EB.
(2)AB=AF+2EB.

-
科目: 来源: 题型:
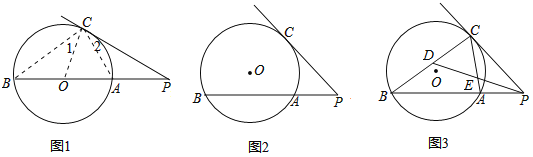
查看答案和解析>>【题目】阅读资料:小明是一个爱动脑筋的好学生,他在学习了有关圆的切线性质后,意犹未尽,又查阅到了与圆的切线相关的一个问题:
如图1,已知PC是⊙O的切线,AB是⊙O的直径,延长BA交切线PC与P,连接AC、BC、OC.
因为PC是⊙O的切线,AB是⊙O的直径,所以∠OCP=∠ACB=90°,所以∠1=∠2.
又因为∠B=∠1,所以∠B=∠2.在△PAC与△PCB中,又因为:∠P=∠P,所以△PAC∽△PCB,所以
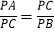 ,即PC2=PAPB.
,即PC2=PAPB.问题拓展:
(Ⅰ)如果PB不经过⊙O的圆心O(如图2)等式PC2=PAPB,还成立吗?请证明你的结论;
综合应用:
(Ⅱ)如图3,⊙O是△ABC的外接圆,PC是⊙O的切线,C是切点,BA的延长线交PC于点P;
(1)当AB=PA,且PC=12时,求PA的值;
(2)D是BC的中点,PD交AC于点E.求证:
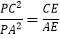 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)求证:BE=CF;
(2)如果AB=8,AC=6,求AE、BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】国家射击队将从甲、乙两名运动员中选拔一人参加奥运会比赛,对他们进行了六次测试,测试成绩如下表:(单位:环)
成绩
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加比赛更合适,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( )
①等角的余角相等;②过一点有且只有一条直线与已知直线平行;③相等的角是对顶角;
④同位角相等;⑤过直线外一点做这条直线的垂线段,则这条垂线段叫做这个点到这条直线的距离.
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】声音在空气中的传播速度v(m/s)与温度t(℃)的关系如下表:
温度(℃)
0
5
10
15
20
速度v(m/s)
331
336
341
346
351
则速度v与温度t之间的关系式为____;当t=30℃时,声音的传播速度为____m/s.
相关试题

