【题目】阅读资料:小明是一个爱动脑筋的好学生,他在学习了有关圆的切线性质后,意犹未尽,又查阅到了与圆的切线相关的一个问题:
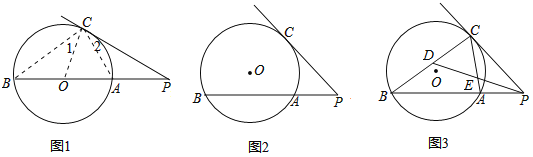
如图1,已知PC是⊙O的切线,AB是⊙O的直径,延长BA交切线PC与P,连接AC、BC、OC.
因为PC是⊙O的切线,AB是⊙O的直径,所以∠OCP=∠ACB=90°,所以∠1=∠2.
又因为∠B=∠1,所以∠B=∠2.
在△PAC与△PCB中,又因为:∠P=∠P,所以△PAC∽△PCB,所以![]() ,即PC2=PAPB.
,即PC2=PAPB.
问题拓展:
(Ⅰ)如果PB不经过⊙O的圆心O(如图2)等式PC2=PAPB,还成立吗?请证明你的结论;
综合应用:
(Ⅱ)如图3,⊙O是△ABC的外接圆,PC是⊙O的切线,C是切点,BA的延长线交PC于点P;
(1)当AB=PA,且PC=12时,求PA的值;
(2)D是BC的中点,PD交AC于点E.求证:![]() .
.
参考答案:
【答案】(Ⅰ)成立,证明见解析;(Ⅱ)(1)6![]() ,(2)证明见解析.
,(2)证明见解析.
【解析】试题分析:(Ⅰ)连接PO并延长交⊙O于点D、E,连接BD、AE,可得△PBD∽△PEA,然后由相似三角形的对应边成比例,可得PAPB=PDPE,再根据PC2=PDPE,即可证得结论。
(Ⅱ)(1)由(Ⅰ)得,PC2=PAPB,即可求得PC2=PAPB=PA(PA+AB)=2PA2,继而即可求得答案;(2)过点A作AF//BC,交PD于点F,由平行线分线段成比例定理,即可得证.
解:(Ⅰ)当PB不经过⊙O的圆心O时,等式PC2=PAPB仍然成立.
如图,连接PO并延长交⊙O于点D,E,连接BD、AE,
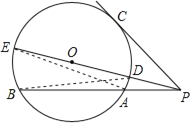
图1
∴∠B=∠E,∠BPD=∠APE,
∴△PBD∽△PEA,
∴![]() ,
,
即PAPB=PDPE,
由图1知,PC2=PDPE,
∴PC2=PAPB.
(Ⅱ)由(1)得,PC2=PAPB,PC=12,AB=PA,
∴PC2=PAPB=PA(PA+AB)=2PA2,
∴2PA2=144,
∴PA=±6![]() (负值无意义,舍去).
(负值无意义,舍去).
∴PA=6![]() .
.
(2)过点A作AF∥BC,交PD于点F,
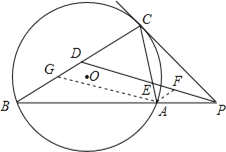
图2
∴![]() ,
,![]() .
.
∵D为BC的中点,
∴BD=CD,
∴![]() ,
,
∴![]() .
.
∵PC2=PAPB,
∴![]() ,
,
即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB两端点A(-1,2),B(4,2),则线段AB上任意一点可表示为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1,x2,x3,x4的方差是a,则3x1﹣5,3x2﹣5,3x3﹣5,3x4﹣5的方差是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
证明:(1)CF=EB.
(2)AB=AF+2EB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)求证:BE=CF;
(2)如果AB=8,AC=6,求AE、BE的长.

-
科目: 来源: 题型:
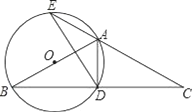
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
(1)求证:D是BC的中点;
(2)若DE=3,BD﹣AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家射击队将从甲、乙两名运动员中选拔一人参加奥运会比赛,对他们进行了六次测试,测试成绩如下表:(单位:环)
成绩
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加比赛更合适,请说明理由.
相关试题

