【题目】某校八年级举行英语演讲比赛,购买A,B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元.根据比赛设奖情况,需购买笔记本共30本,并且所购买A笔记本的数量要不多于B笔记本数量的![]() ,但又不少于B笔记本数量
,但又不少于B笔记本数量![]() ,设买A笔记本n本,买两种笔记本的总费为w元.
,设买A笔记本n本,买两种笔记本的总费为w元.
(1)写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;
(2)购买这两种笔记本各多少时,费用最少?最少的费用是多少元?
(3)商店为了促销,决定仅对A种类型的笔记本每本让利a元销售,B种类型笔记本售价不变.问购买这两种笔记本各多少本时花费最少?
参考答案:
【答案】(1)5≤n≤![]() ;(2)当n=5时,w取到最小值为260元;(3)当4﹣a>0,即a<4时,n=5,即买A笔记本5本,B笔记本25本,花费最少;当4﹣a=0,即a=4时,5≤n≤13,即买A笔记本5﹣13本,B笔记本25﹣17本,花费为240元;当4﹣a<0,即a>4时,n=13,即买A笔记本13本,B笔记本17本,花费最少.
;(2)当n=5时,w取到最小值为260元;(3)当4﹣a>0,即a<4时,n=5,即买A笔记本5本,B笔记本25本,花费最少;当4﹣a=0,即a=4时,5≤n≤13,即买A笔记本5﹣13本,B笔记本25﹣17本,花费为240元;当4﹣a<0,即a>4时,n=13,即买A笔记本13本,B笔记本17本,花费最少.
【解析】
(1)根据题意得到w(元)关于n(本)的函数关系式,可得到一个关于n的不等式组,可求出n的取值范围,再结合花费的函数式,可求出x的具体数值;
(2)结合花费的函数式,可求出x的具体数值;
(3)根据a的取值范围即可得到结论.
解:(1)由题意可知:w=12n+8(30﹣n),
∴w=4n+240,
又∵A笔记本的数量要不多于B笔记本数量的![]() ,但又不少于B笔记本数量的
,但又不少于B笔记本数量的![]() .
.
∴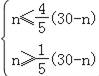 ,解得5≤n≤
,解得5≤n≤![]() ,
,
(2)w=4n+240,
∵k=4>0,
∴w随n的增大而增大,
∴当n=5时,w取到最小值为260元.
(3)w=(12﹣a)n+8(30﹣n),
∴w=(4﹣a)n+240,
当4﹣a>0,即a<4时,n=5,即买A笔记本5本,B笔记本25本,花费最少,
当4﹣a=0,即a=4时,5≤n≤13,即买A笔记本5﹣13本,B笔记本25﹣17本,花费为240元,
当4﹣a<0,即a>4时,n=13,即买A笔记本13本,B笔记本17本,花费最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列美丽的图案,是轴对称图形但不是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数
1
2
3
4
5
6
7
8
9
10
黑棋数
1
3
0
2
3
4
2
1
1
3
根据以上数据,估算袋中的白棋子数量为( )
A.60枚
B.50枚
C.40枚
D.30枚 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形ABCD沿直线EF折叠,若∠1=20°,则∠2=( )
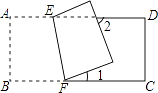
A.80°
B.70°
C.40°
D.20° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作
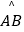 .过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 .
.过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 . 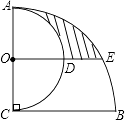
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,AB=4,BC=5,∠ABC=60°,对角线AC,BD交于点O,过点O作OE⊥AD,则OE等于( )

A.
B.2
C.2
D.2.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)

相关试题

