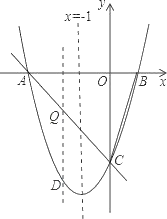
【题目】如图:对称轴x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,其中点A的坐标为(﹣3,0),且点(2,5)在抛物线y=ax2+bx+c上.
(1)求抛物线的解析式.
(2)点C为抛物线与y轴的交点.
①点P在抛物线上,且S△POC=4S△BOC,求点P点坐标.
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
参考答案:
【答案】(1)抛物线的解析式为:y=x2+2x﹣3;
(2)①点P的坐标为(4,21)或(﹣4,5);
②当x=﹣![]() 时,QD有最大值
时,QD有最大值![]() .
.
【解析】试题分析:(1)因为抛物线的对称轴为x=-1,A点坐标为(-3,0)与(2,5)在抛物线上,代入抛物线的解析式,即可解答;(2)①先由二次函数的解析式为y=x2+2x-3,得到C点坐标,然后设P点坐标为(x,x2+2x-3),根据S△POC=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;②先运用待定系数法求出直线AC的解析式为y=-x-3,再设Q点坐标为(x,-x-3),则D点坐标为(x,x2+2x-3),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.
试题解析:(1)因为抛物线的对称轴为x=﹣1,A点坐标为(﹣3,0)与(2,5)在抛物线上,则:
 ,
,
解得: 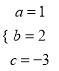 .
.
所以抛物线的解析式为:y=x2+2x﹣3.
(2)①二次函数的解析式为y=x2+2x﹣3,
∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3.
设P点坐标为(x,x2+2x﹣3),
∵S△POC=4S△BOC,
∴![]() ×3×|x|=4×
×3×|x|=4×![]() ×3×1,
×3×1,
∴|x|=4,x=±4.当x=4时,x2+2x﹣3=16+8﹣3=21;
当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5.
∴点P的坐标为(4,21)或(﹣4,5);
②设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,﹣3)代入,
得![]() ,
,
解得: ![]() .
.
即直线AC的解析式为y=﹣x﹣3.
设Q点坐标为(x,﹣x﹣3)(﹣3≤x≤0),则D点坐标为(x,x2+2x﹣3),
QD=(﹣x﹣3)﹣(x2+2x﹣3)=﹣x2﹣3x=﹣![]() ,
,
∴当x=﹣![]() 时,QD有最大值
时,QD有最大值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点(-2,-3)向上平移3个单位长度,则平移后的点的坐标为( )
A. (-2,0) B. (-2,1) C. (0,-2) D. (1,-1)
-
科目: 来源: 题型:
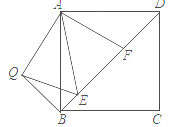
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个实数的算术平方根与它的立方根相等,则这个数是( )
A.0B.正整数C.0和1D.1
-
科目: 来源: 题型:
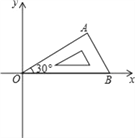
查看答案和解析>>【题目】将含有30°角的直角三角板OAB按如图所示的方式放置在平面直角坐标系中,OB在x轴上,若OA=4,将三角板绕原点O逆时针旋转,每秒旋转60°,则第2017秒时,点A的对应点A′的坐标为( )
A. (0,4) B. (2
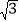 ,﹣2) C. (﹣2
,﹣2) C. (﹣2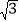 ,2) D. (0,﹣4)
,2) D. (0,﹣4) -
科目: 来源: 题型:
查看答案和解析>>【题目】若(3x+a)(3x+b)的结果中不含有x项,则a、b的关系是( )
A.ab=1
B.ab=0
C.a﹣b=0
D.a+b=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+a)(x+b)的结果中不含有x的一次项,则a、b的关系是( )
A.ab=1
B.ab=0
C.a﹣b=0
D.a+b=0
相关试题

