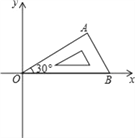
【题目】将含有30°角的直角三角板OAB按如图所示的方式放置在平面直角坐标系中,OB在x轴上,若OA=4,将三角板绕原点O逆时针旋转,每秒旋转60°,则第2017秒时,点A的对应点A′的坐标为( )
A. (0,4) B. (2![]() ,﹣2) C. (﹣2
,﹣2) C. (﹣2![]() ,2) D. (0,﹣4)
,2) D. (0,﹣4)
参考答案:
【答案】A
【解析】∵OA=4,∠AOB=30°,将三角板绕原点O逆时针旋转,每秒旋转60°,
∴第1秒时,点A的对应点A′的坐标为(0,4).
∵三角板每秒旋转60°,
∴点A′的位置6秒一循环.
∵2017=336×6+1,
∴第2017秒时,点A的对应点A′的坐标为(0,4).
故选A.
点睛:本题考查了坐标与图形的变化中的旋转以及规律型中点的坐标,根据每秒旋转的角度,找出点A′的位置6秒一循环是解题的关键.
-
科目: 来源: 题型:
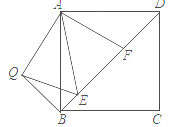
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个实数的算术平方根与它的立方根相等,则这个数是( )
A.0B.正整数C.0和1D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:对称轴x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,其中点A的坐标为(﹣3,0),且点(2,5)在抛物线y=ax2+bx+c上.
(1)求抛物线的解析式.
(2)点C为抛物线与y轴的交点.
①点P在抛物线上,且S△POC=4S△BOC,求点P点坐标.
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(3x+a)(3x+b)的结果中不含有x项,则a、b的关系是( )
A.ab=1
B.ab=0
C.a﹣b=0
D.a+b=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+a)(x+b)的结果中不含有x的一次项,则a、b的关系是( )
A.ab=1
B.ab=0
C.a﹣b=0
D.a+b=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】在下列说法中,正确的是( )
A.如果两个三角形全等,则它们必是关于直线成轴对称的图形
B.如果两个三角形关于某直线成轴对称,那么它们是全等三角形
C.等腰三角形是关于底边中线成轴对称的图形
D.一条线段是关于经过该线段中点的直线成轴对称的图形
相关试题

