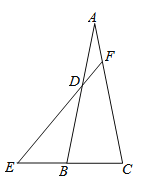
【题目】如图,△ABC是等腰三角形,AB=AC=3,BC=1.点D在AB边上,点E在CB的延长线上,已知AD=1,BE=1,连接ED并延长交AC于点F,则线段AF的长为_________.
参考答案:
【答案】![]()
【解析】
取CF的中点G,连接BG,证出BG是△CEF的中位线,由三角形中位线定理得出BG∥EF,证出△ADF∽△ABG,得出比例式![]() ,因此AF=
,因此AF=![]() AG,∴FG=CG=2AF,得出AC=AF+FG+CG=5AF=3,即可得出AF的长.
AG,∴FG=CG=2AF,得出AC=AF+FG+CG=5AF=3,即可得出AF的长.
取CF的中点G,连接BG,如图所示:
∵BC=1,BE=1,
∴点B为EC的中点,
∴BG是△CEF的中位线,
∴BG∥EF,
∴![]() ,
,
∴AF=![]() AG,
AG,
∴FG=CG=2AF,
∴AC=AF+FG+CG=5AF=3,
∴AF=![]() ;
;
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
-
科目: 来源: 题型:
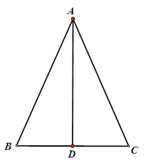
查看答案和解析>>【题目】求证:角平分线和中线重合的三角形是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
 中,
中, ,垂足为点H,若
,垂足为点H,若 ,
, ,则
,则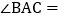 ______
______
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了增强学生体质,开设了体育活动小组,并计划购买一些篮球和排球
 已知每个篮球的售价比每个排球的售价多20元,用1100元购进的篮球数量是用450元购进排球数量的2倍.
已知每个篮球的售价比每个排球的售价多20元,用1100元购进的篮球数量是用450元购进排球数量的2倍. 求每个篮球和每个排球的单价各是多少元;
求每个篮球和每个排球的单价各是多少元; 若学校计划购进篮球和排球共50个,且购进的总费用不超过4900元,则学校最多可以购进篮球多少个?
若学校计划购进篮球和排球共50个,且购进的总费用不超过4900元,则学校最多可以购进篮球多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为贯彻落实十九大会议精神,践行“绿水青山就是金山银山”的发展理念,积极推动生态文明理念融入学校教育,某中学拟举办“爱家乡、览名山”活动,围绕“哈尔滨市周边五大名山,即:香炉山、凤凰山、金龙山、帽儿山、二龙山,你最喜欢那一座山?
 每名学生必选且只选一座山
每名学生必选且只选一座山 ”的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图所示的不完整统计图
”的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图所示的不完整统计图 请根据统计图的信息回答下列问题:
请根据统计图的信息回答下列问题: 本次调查共抽取了多少名学生?
本次调查共抽取了多少名学生? 求本次调查中,最喜欢风凰山的学生人数,并补全条形统计图;
求本次调查中,最喜欢风凰山的学生人数,并补全条形统计图; 若该中学共有学生1200人,请你估计该中学最喜欢香炉山的学生约有多少人.
若该中学共有学生1200人,请你估计该中学最喜欢香炉山的学生约有多少人.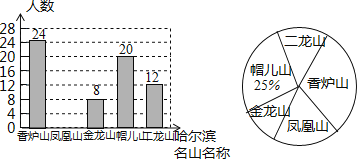
相关试题

