【题目】平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=0D=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).
发现:
(1)当α=0°,即初始位置时,点P直线AB上.(填“在”或“不在”)求当α是多少时,OQ经过点B.
(2)在OQ旋转过程中,简要说明α是多少时,点P,A间的距离最小?并指出这个最小值;
(3)如图2,当点P恰好落在BC边上时,求a及S阴影
拓展:
如图3,当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.
探究:当半圆K与矩形ABCD的边相切时,求sinα的值.
参考答案:
【答案】
(1)在
(2)解:如图2,连接AP,
∵OA+AP≥OP,
当OP过点A,即α=60°时,等号成立,
∴AP≥OP﹣OA=2﹣1=1,
∴当α=60°时,P、A之间的距离最小,
∴PA的最小值=1
(3)解:如图2,
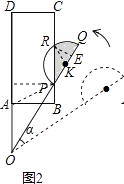
设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H,
过点R作RE⊥KQ于点E,在Rt△OPH中,PH=AB=1,OP=2,
∴∠POH=30°,
∴α=60°﹣30°=30°,
∵AD∥BC,
∴∠RPO=∠POH=30°,
∴∠RKQ=2×30°=60°,
∴S扇形KRQ= ![]() =
= ![]() ,
,
在Rt△RKE中,RE=RKsin60°= ![]() ,
,
∴S△PRK= ![]() RE=
RE= ![]() ,∴S阴影=
,∴S阴影= ![]() +
+ ![]() ;
;
拓展:如图5,
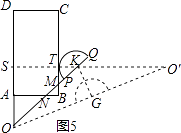
∵∠OAN=∠MBN=90°,∠ANO=∠BNM,
∴△AON∽△BMN,
∴ ![]() ,即
,即 ![]() ,
,
∴BN= ![]() ,
,
如图4,
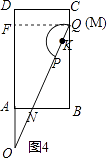
当点Q落在BC上时,x取最大值,作QF⊥AD于点F,BQ=AF= ![]() ﹣AO=2
﹣AO=2 ![]() ﹣1,
﹣1,
∴x的取值范围是0<x≤2 ![]() ﹣1;
﹣1;
探究:半圆K与矩形ABCD的边相切,分三种情况;
①如图5,半圆K与BC相切于点T,设直线KT与AD,OQ的初始位置所在的直线分别交于点S,O′,
则∠KSO=∠KTB=90°,
作KG⊥OO′于G,在Rt△OSK中,
OS= ![]() =2,
=2,
在Rt△OSO′中,SO′=OStan60°=2 ![]() ,KO′=2
,KO′=2 ![]() ﹣
﹣ ![]() ,
,
在Rt△KGO′中,∠O′=30°,
∴KG= ![]() KO′=
KO′= ![]() ﹣
﹣ ![]() ,
,
∴在Rt△OGK中,sinα= ![]() =
= ![]() =
= ![]() ,
,
②当半圆K与AD相切于T,如图6,
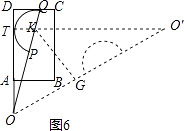
同理可得sinα= 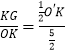 =
= 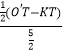 =
= ![]() =
= ![]() ;
;
③当半圆K与CD切线时,点Q与点D重合,且为切点,
∴α=60°,
∴sinα=sin60 ![]() ,
,
综上所述sinα的值为: ![]() 或
或 ![]() 或
或 ![]() .
.
【解析】解:发现:(1)在,
当OQ过点B时,在Rt△OAB中,AO=AB,
∴∠DOQ=∠ABO=45°,
∴α=60°﹣45°=15°;
(1)在,当OQ过点B时,在Rt△OAB中,AO=AB,得到∠DOQ=∠ABO=45°,求得α=60°﹣45°=15°;(2)如图2,连接AP,由OA+AP≥OP,当OP过点A,即α=60°时,等号成立,于是有AP≥OP﹣OA=2﹣1=1,当α=60°时,P、A之间的距离最小,即可求得结果(3)如图2,设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H,过点R作RE⊥KQ于点E,在Rt△OPH中,PH=AB=1,OP=2,得到∠POH=30°,求得α=60°﹣30°=30°,由于AD∥BC,得到∠RPO=∠POH=30°,求出∠RKQ=2×30°=60°,于是得到结果;
拓展:如图5,由∠OAN=∠MBN=90°,∠ANO=∠BNM,得到△AON∽△BMN求出BN= ![]() ,如图4,当点Q落在BC上时,x取最大值,作QF⊥AD于点F,BQ=AF=
,如图4,当点Q落在BC上时,x取最大值,作QF⊥AD于点F,BQ=AF= ![]() ﹣AO=2
﹣AO=2 ![]() ﹣1,求出x的取值范围是0<x≤2
﹣1,求出x的取值范围是0<x≤2 ![]() ﹣1;
﹣1;
探究:半圆K与矩形ABCD的边相切,分三种情况;
①如图5,半圆K与BC相切于点T,设直线KT与AD,OQ的初始位置所在的直线分别交于点S,O′,于是得到∠KSO=∠KTB=90°,作KG⊥OO′于G,在Rt△OSK中,求出OS= ![]() =2,在Rt△OSO′中,SO′=OStan60°=2
=2,在Rt△OSO′中,SO′=OStan60°=2 ![]() ,KO′=2
,KO′=2 ![]() ﹣
﹣ ![]() 在Rt△KGO′中,∠O′=30°,求得KG=
在Rt△KGO′中,∠O′=30°,求得KG= ![]() KO′=
KO′= ![]() ﹣
﹣ ![]() ,在Rt△OGK中,求得结果;②当半圆K与AD相切于T,图6,同理可得sinα的值③当半圆K与CD切线时,点Q与点D重合,且为切点,得到α=60°于是结论可求.
,在Rt△OGK中,求得结果;②当半圆K与AD相切于T,图6,同理可得sinα的值③当半圆K与CD切线时,点Q与点D重合,且为切点,得到α=60°于是结论可求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)探究规律:如图,已知□ABCD,试用三种方法将它分成面积相等的两部分:



(2)解决问题:兄弟俩共同承包的一块平行四边形的土地,现要进行平均划分,由于在这块地里有一口水井P,如图所示,为了兄弟俩都能方便使用这口井,兄弟俩在划分时犯难了,聪明的你能帮他们解决这个问题吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”.
(1)求函数y=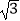 x+2的图象上所有“中国结”的坐标;
x+2的图象上所有“中国结”的坐标;
(2)若函数y=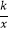 (k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(3)若二次函数y=(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k(k为常数)的图象与x轴相交得到两个不同的“中国结”,试问该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”? -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车为一家摩托车配件批发部送货,先向南走了8km到达“华能”修理部,又向北走了3.5km到达“捷速”修理部,继续向北走了7.5km到达“志远”修理部,最后又回到了批发部.
(1)以批发部为原点,以向南的方向为正方向,用1个单位长度表示1km,你能在数轴上表示出“华能”、“捷速”、“志远”三家修理部的位置吗?
(2)“志远”修理部到“捷速”修理部多远?
(3)货车若行驶1千米需耗油0.5升,本次这辆货车共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)当
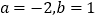 时,求两个代数式
时,求两个代数式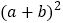 与
与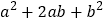 的值;
的值;(2)当
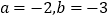 时,再求以上两个代数式的值;
时,再求以上两个代数式的值;(3)你能从上面的计算结果中,发现上面有什么结论?
结论是: ;
-
科目: 来源: 题型:
查看答案和解析>>【题目】用锤子以均匀的力敲击铁钉入木板.随着铁钉的深入,铁钉所受的阻力会越来越大,使得每次钉入木板的钉子的长度后一次为前一次的k倍(0<k<1).已知一个钉子受击3次后恰好全部进入木板,且第一次受击后进入木板部分的铁钉长度是钉长的
 .设铁钉的长度为1,那么符合这一事实的方程是( )
.设铁钉的长度为1,那么符合这一事实的方程是( )
A.
(1+k)2=1
B.
k+ k2=1
k2=1
C.
+ k+
k+  k2=1
k2=1
D.
+ (1+k)2=1
(1+k)2=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】利用平方根去根号可以构造一个整系数方程.例如:x=
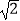 +1时,移项得x﹣1=
+1时,移项得x﹣1= 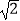 ,两边平方得(x﹣1)2=(
,两边平方得(x﹣1)2=( 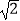 )2 , 所以x2﹣2x+1=2,即x2﹣2x﹣1=0.仿照上述构造方法,当x=
)2 , 所以x2﹣2x+1=2,即x2﹣2x﹣1=0.仿照上述构造方法,当x= 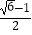 时,可以构造出一个整系数方程是( )
时,可以构造出一个整系数方程是( )
A.4x2+4x+5=0
B.4x2+4x﹣5=0
C.x2+x+1=0
D.x2+x﹣1=0
相关试题

