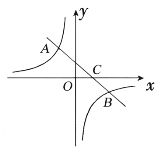
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于二、四象限内的
的图象交于二、四象限内的![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
(1)求该反比例函数和一次函数的解析式;
(2)连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
(3)设点![]() 在
在![]() 轴上,且满足
轴上,且满足![]() 是直角三角形,直接写出点
是直角三角形,直接写出点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)9;(3)存在,满足条件的
;(2)9;(3)存在,满足条件的![]() 点坐标为
点坐标为![]()
【解析】
(1)先把A(-3,4)代入反比例函数解析式得到m的值,从而确定反比例函数的解析式为y=![]() ;再利用反比例函数解析式确定B点坐标为(6,-2),然后运用待定系数法确定所求的一次函数的解析式为y=
;再利用反比例函数解析式确定B点坐标为(6,-2),然后运用待定系数法确定所求的一次函数的解析式为y=![]() ;
;
(2)先依据一次函数求得点C的坐标,进而得到△AOB 的面积;
(3)过A点作AP1⊥x轴交x轴于P1,AP2⊥AC交x轴于P2,即可得P1点的坐标为(-3,0);再证明Rt△AP2P1∽Rt△CAP1,利用相似比计算出P1P2的长度,进而得到OP2的长度,可得P2点的坐标为![]() ,于是得到满足条件的P点坐标.
,于是得到满足条件的P点坐标.
(1)将![]() 代入
代入![]() ,得
,得![]() .
.
∴反比例函数的解析式为![]() ,
,
将![]() 代入
代入![]() ,
,
得![]()
解得![]()
∴![]()
将![]() 分别代入
分别代入![]() ,得
,得
![]() ,解得
,解得
∴所求的一次函数的解析式为![]()
(2)当![]() 时,
时,![]() ,
,
解得:![]() ,
,
![]()
![]()
∴![]()
(3)存在
∴满足条件的![]() 点坐标为
点坐标为![]() ,理由如下:
,理由如下:
过A点作AP1⊥x轴于P1,AP2⊥AC交x轴于P2,如图,
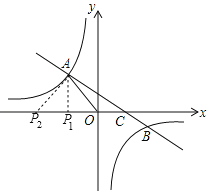
∴∠AP1C=90°,
∵A点坐标为(-3,4),
∴P1点的坐标为(-3,0);
∵∠P2AC=90°,
∴∠P2AP1+∠P1AC=90°,而∠AP2P1+∠P2AP1=90°,
∴∠AP2P1=∠P1AC,
∴Rt△AP2P1∽Rt△CAP1,
∴![]() ,即
,即![]() ,
,
∴P1P2=![]() ,
,
∴OP2=3+![]() =
=![]() ,
,
∴P2点的坐标为(![]() ,0),
,0),
∴满足条件的P点坐标为(-3,0)、(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某童装专卖店在销售中发现,一款童装每件进价为40元,若销售价为60元,每天可售出20件,为迎接“双十一”,专卖店决定采取适当的降价措施,以扩大销售量,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件
 设每件童装降价x元
设每件童装降价x元 时,平均每天可盈利y元.
时,平均每天可盈利y元. 写出y与x的函数关系式;
写出y与x的函数关系式; 当该专卖店每件童装降价多少元时,平均每天盈利400元?
当该专卖店每件童装降价多少元时,平均每天盈利400元?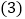 该专卖店要想平均每天盈利600元,可能吗?请说明理由.
该专卖店要想平均每天盈利600元,可能吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】文具店有三种品牌的6个笔记本,价格是4,5,7(单位:元)三种,从中随机拿出一个本,已知
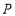 (一次拿到7元本)
(一次拿到7元本)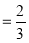 .
.(1)求这6个本价格的众数.
(2)若琪琪已拿走一个7元本,嘉嘉准备从剩余5个本中随机拿一个本.
①所剩的5个本价格的中位数与原来6个本价格的中位数是否相同?并简要说明理由;
②嘉嘉先随机拿出一个本后不放回,之后又随机从剩余的本中拿一个本,用列表法求嘉嘉两次都拿到7元本的概率.
-
科目: 来源: 题型:
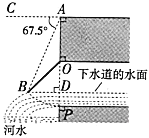
查看答案和解析>>【题目】如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中
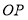 为下水管道口直径,
为下水管道口直径, 为可绕转轴
为可绕转轴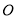 自由转动的阀门,平时阀门被管道中排出的水冲开,可排出城市污水:当河水上涨时,阀门会因河水压迫而关闭,以防止河水倒灌入城中.若阀门的直径
自由转动的阀门,平时阀门被管道中排出的水冲开,可排出城市污水:当河水上涨时,阀门会因河水压迫而关闭,以防止河水倒灌入城中.若阀门的直径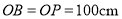 ,
,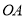 为检修时阀门开启的位置,且
为检修时阀门开启的位置,且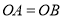 .
.
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中
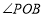 的取值范围;
的取值范围;(2)为了观测水位,当下水道的水冲开阀门到达
 位置时,在点
位置时,在点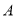 处测得俯角
处测得俯角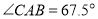 ,若此时点
,若此时点 恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留根号)
恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
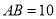 ,以
,以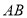 为直径作半圆
为直径作半圆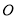 ,半径
,半径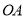 绕点
绕点 顺时针旋转得到
顺时针旋转得到 ,点
,点 的对应点为
的对应点为 ,当点
,当点 与点
与点 重合时停止.连接
重合时停止.连接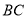 并延长到点
并延长到点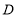 ,使得
,使得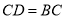 ,过点
,过点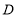 作
作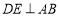 于点
于点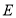 ,连接
,连接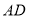 ,
,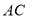 .
.(1)
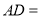 ______;
______;(2)如图,当点
 与点
与点 重合时,判断
重合时,判断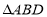 的形状,并说明理由;
的形状,并说明理由;
(3)如图,当
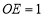 时,求
时,求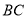 的长;
的长;
(4)如图,若点
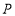 是线段
是线段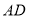 上一点,连接
上一点,连接 ,当
,当 与半圆
与半圆 相切时,直接写出直线
相切时,直接写出直线 与
与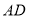 的位置关系.
的位置关系.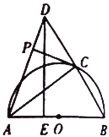
-
科目: 来源: 题型:
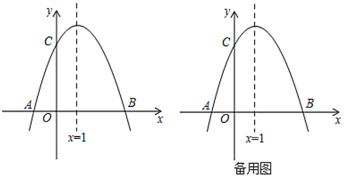
查看答案和解析>>【题目】如图,已知抛物线
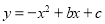 与
与 轴交于
轴交于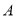 、
、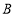 两点,
两点,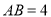 ,交
,交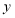 轴于点
轴于点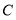 ,对称轴是直线
,对称轴是直线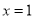 .
.
(1)求抛物线的解析式及点
 的坐标;
的坐标;(2)连接
 ,
,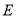 是线段
是线段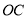 上一点,
上一点,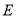 关于直线
关于直线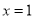 的对称点
的对称点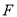 正好落在
正好落在 上,求点
上,求点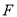 的坐标;
的坐标;(3)动点
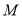 从点
从点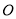 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点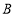 运动,过
运动,过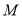 作
作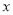 轴的垂线交抛物线于点
轴的垂线交抛物线于点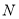 ,交线段
,交线段 于点
于点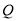 .设运动时间为
.设运动时间为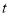 (
(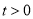 )秒.若
)秒.若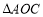 与
与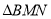 相似,请求出
相似,请求出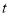 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )
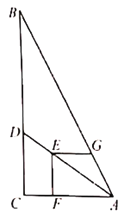
A.3.6B.4C.4.8D.5
相关试题

