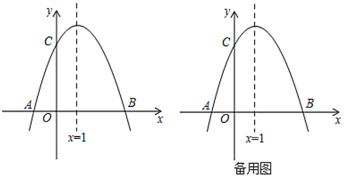
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,交
,交![]() 轴于点
轴于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,
上一点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() (
(![]() )秒.若
)秒.若![]() 与
与![]() 相似,请求出
相似,请求出![]() 的值.
的值.
参考答案:
【答案】(1)![]() ,
,![]() 点坐标为
点坐标为![]() ;(2)F
;(2)F![]() ;(3)
;(3)![]()
【解析】
(1)先求出点A,B的坐标,将A、B的坐标代入![]() 中,即可求解;
中,即可求解;
(2)确定直线BC的解析式为y=x+3,根据点E、F关于直线x=1对称,即可求解;
(3) 若![]() 与
与![]() 相似,则
相似,则![]() 或
或![]() ,即可求解;
,即可求解;
解:(1)∵点![]() 、
、![]() 关于直线
关于直线![]() 对称,
对称,![]() ,∴
,∴![]() ,
,![]() .
.
代入![]() 中,得:
中,得:![]() ,解
,解![]() ,
,
∴抛物线的解析式为![]() .
.
∴![]() 点坐标为
点坐标为![]() ;
;
(2)设直线![]() 的解析式为
的解析式为![]() ,则有:
,则有:![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
∵点![]() 、
、![]() 关于直线
关于直线![]() 对称,
对称,
又![]() 到对称轴的距离为1,∴
到对称轴的距离为1,∴![]() .
.
∴![]() 点的横坐标为2,将
点的横坐标为2,将![]() 代入
代入![]() 中,得:
中,得:![]() ,
,
∴F(2,1);
(3)![]() 秒时,
秒时,![]() .如图
.如图
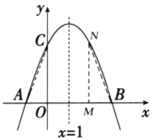
当![]() 时
时
![]()
![]()
∴![]() ,∴
,∴![]() ,
,
![]() .
.
①若![]() ,则
,则![]() ,即
,即![]()
![]() (舍去),或
(舍去),或![]() .
.
②若![]() ,则
,则![]() ,即
,即![]()
![]() (舍去),或
(舍去),或![]() (舍去)
(舍去)
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中
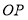 为下水管道口直径,
为下水管道口直径, 为可绕转轴
为可绕转轴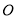 自由转动的阀门,平时阀门被管道中排出的水冲开,可排出城市污水:当河水上涨时,阀门会因河水压迫而关闭,以防止河水倒灌入城中.若阀门的直径
自由转动的阀门,平时阀门被管道中排出的水冲开,可排出城市污水:当河水上涨时,阀门会因河水压迫而关闭,以防止河水倒灌入城中.若阀门的直径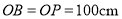 ,
, 为检修时阀门开启的位置,且
为检修时阀门开启的位置,且 .
.
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中
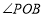 的取值范围;
的取值范围;(2)为了观测水位,当下水道的水冲开阀门到达
 位置时,在点
位置时,在点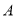 处测得俯角
处测得俯角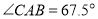 ,若此时点
,若此时点 恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留根号)
恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
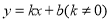 的图象与反比例函数
的图象与反比例函数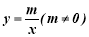 的图象交于二、四象限内的
的图象交于二、四象限内的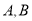 两点,与
两点,与 轴交于
轴交于 点,点
点,点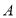 的坐标为
的坐标为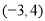 ,点
,点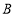 的坐标为
的坐标为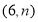
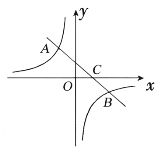
(1)求该反比例函数和一次函数的解析式;
(2)连接
 、
、 ,求
,求 的面积;
的面积;(3)设点
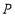 在
在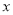 轴上,且满足
轴上,且满足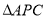 是直角三角形,直接写出点
是直角三角形,直接写出点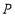 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
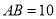 ,以
,以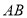 为直径作半圆
为直径作半圆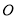 ,半径
,半径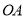 绕点
绕点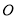 顺时针旋转得到
顺时针旋转得到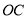 ,点
,点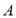 的对应点为
的对应点为 ,当点
,当点 与点
与点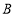 重合时停止.连接
重合时停止.连接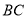 并延长到点
并延长到点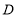 ,使得
,使得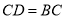 ,过点
,过点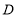 作
作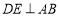 于点
于点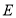 ,连接
,连接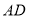 ,
,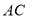 .
.(1)
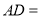 ______;
______;(2)如图,当点
 与点
与点 重合时,判断
重合时,判断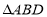 的形状,并说明理由;
的形状,并说明理由;
(3)如图,当
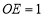 时,求
时,求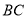 的长;
的长;
(4)如图,若点
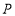 是线段
是线段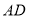 上一点,连接
上一点,连接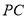 ,当
,当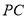 与半圆
与半圆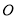 相切时,直接写出直线
相切时,直接写出直线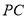 与
与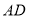 的位置关系.
的位置关系.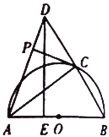
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )
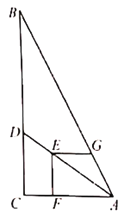
A.3.6B.4C.4.8D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,P为CD的中点,连结AP,过点B作BE⊥AP于点E,延长CE交AD于点F,过点C作CH⊥BE于点G,交AB于点H,连接HF.下列结论正确的是( )

A. CE=
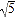 B. EF=
B. EF=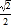 C. cos∠CEP=
C. cos∠CEP=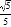 D. HF2=EFCF
D. HF2=EFCF -
科目: 来源: 题型:
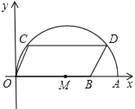
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为______.
相关试题

