搜索
【题目】实践与探索
（1）填空： 
=； 
=；
（2）观察第（1）的结果填空：当a≥0时 
=；当a＜0时， =；
（3）利用你总结的规律计算： 
+ 
，其中2＜x＜3．
参考答案：
【答案】
（1）3；5
（2）a；﹣a
（3）解：∵2＜x＜3，
∴x﹣2＞0、x﹣3＜0，
原式=（x﹣2 ）﹣（x﹣3）
=1
【解析】解：（1） 
=3； 
=5； 所以答案是：3，5；
⑵当a≥0时 
=a；当a＜0时， =﹣a；
所以答案是：a，﹣a；
【考点精析】关于本题考查的二次根式的性质与化简，需要了解1、如果被开方数是分数（包括小数）或分式，先利用商的算数平方根的性质把它写成分式的形式，然后利用分母有理化进行化简．2、如果被开方数是整数或整式，先将他们分解因数或因式，然后把能开得尽方的因数或因式开出来才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明在课外学习时遇到这样一个问题：
定义：如果二次函数
是常数与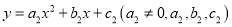
是常数）满足
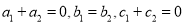，则称这两个函数互为“旋转函数”．求函数
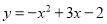的 “旋转函数”．小明是这样思考的：由
函数可知a1=-1，b1=3，c1=-3，根据a1+a2=0，b1=b2，c1+c2=0求出a2,b2,c2，就能确定这个函数的“旋转函数”．请参考小明的方法解决下面的问题：
（1）写出函数
的“旋转函数”；（2）若函数
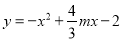与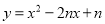
互为“旋转函数”，求（m+n）2017的值；（3）已知函数
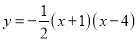的图象与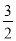
轴交于A、B两点，与y轴交于点C，点A、B、C关于原点的对称点分别是A1、B1、C1，试证明经过点A1、B1、C1的二次函数与函数
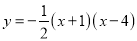互为“旋转函数”． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题：①直径相等的两个圆是等圆；②等弧是长度相等的弧；③圆中最长的弦是通过圆心的弦； ④一条弦把圆分为两条弧，这两条弧不可能是等弧．其中真命题是 ( )
A. ①③B. ①③④C. ①②③D. ②④
-
科目： 来源： 题型：
查看答案和解析>>【题目】方程（m﹣2）xm(m-3)+4+3mx﹣1＝0是关于x的一元二次方程，则m＝____________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，DE分别是AB，AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连CF
（1）求证：四边形BCFE是菱形；
（2）若CE=6，∠BEF=120°，求菱形BCFE的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】写出一个一元一次方程：_____________，它的解是x=-2.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边由长为30米的篱笆围成．已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边长为x米．
（1）若苗圃园的面积为72平方米，求x；
（2）若平行于墙的一边长不小于8米，这个苗圃园的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由．
相关试题
