Question

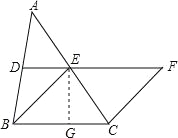
【题目】如图，在△ABC中，DE分别是AB，AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连CF

（1）求证：四边形BCFE是菱形；

（2）若CE=6，∠BEF=120°，求菱形BCFE的面积．

Answer 1

【答案】（1）证明见解析（2）18

【解析】从所给的条件可知，DE是△ABC中位线，所以DE∥BC且2DE=BC，所以BC和EF平行且相等，所以四边形BCFE是平行四边形，又因为BE=FE，所以是菱形；∠BCF是120°，所以∠EBC为60°，所以菱形的边长也为６，求出菱形的高面积就可求．

解：（1）证明：∵D、E分别是AB、AC的中点，

∴DE∥BC且2DE=BC，

又∵BE=2DE，EF=BE，

∴EF=BC，EF∥BC，

∴四边形BCFE是平行四边形，

又∵BE=EF，

∴四边形BCFE是菱形；

（2）解：∵∠BEF=120°，

∴∠EBC=60°，

∴△EBC是等边三角形，

∴BE=BC=CE=6，

过点E作EG⊥BC于点G，

∴EG=BEsin60°=6×=3，

∴S菱形BCFE=BCEG=6×3=18．

“点睛”本题考查菱形的判定和性质以及三角形中位线定理，以及菱形的面积的计算等知识点．