Question

【题目】如图，已知点D为等腰直角△ABC内一点，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA．

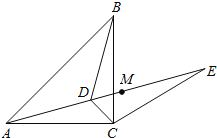
（1）求证：DE平分∠BDC；

（2）若点M在DE上，且DC=DM，求证：ME=BD．

Answer 1

【答案】（1）证明见解析；（2）证明见解析

【解析】

试题分析：（1）根据△ABC是等腰直角三角形得出∠BAC=∠ABC=45°，根据∠CAD=∠CBD=15°得出∠BAD=∠ABD=30°，则BD=AD，说明D在AB的垂直平分线上，根据AC=BC得出点C也在AB的垂直平分线上，从而说明直线CD是AB的垂直平分线，则∠ACD=∠BCD=45°，∠CDE=∠BDE=60°，即DE平分∠BDC；（2）连接MC，根据DC=DM，∠MDC=60°得到△MDC为正三角形，则CM=CD，∠DMC=∠MDC=60°，从而得到∠DAC=∠CEM，从而说明△ADC和△EMC全等，则ME=AD=BD．

试题解析：（1）∵△ABC是等腰直角三角形， ∴∠BAC=∠ABC=45°， ∵∠CAD=∠CBD=15°，

∴∠BAD=∠ABD=45°﹣15°=30°， ∠ABD=∠ABC﹣15°=30°， ∴∠BAD=∠ABD ∴BD=AD，

∴D在AB的垂直平分线上， ∵AC=BC， ∴C也在AB的垂直平分线上， 即直线CD是AB的垂直平分线，

∴∠ACD=∠BCD=45°， ∴∠CDE=15°+45°=60°， ∴∠BDE=∠DBA+∠BAD=60°； ∴∠CDE=∠BDE，

即DE平分∠BDC．

（2）如图，连接MC．

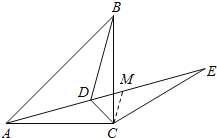
∵DC=DM，且∠MDC=60°， ∴△MDC是等边三角形，

∴CM=CD．∠DMC=∠MDC=60°， ∵∠ADC+∠MDC=180°，∠DMC+∠EMC=180°， ∴∠EMC=∠ADC．

又∵CE=CA， ∴∠DAC=∠CEM．

在△ADC与△EMC中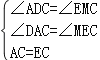，， ∴△ADC≌△EMC（AAS）， ∴ME=AD=BD．