【题目】已知一次函数y=kx+b 的图象与反比例函数y=![]() 的图交象于A、B两点,且点A的横坐标和点B的纵坐标都是-2 , 求:
的图交象于A、B两点,且点A的横坐标和点B的纵坐标都是-2 , 求:
(1)一次函数的解析式;
(2)△AOB的面积
参考答案:
【答案】(1)y=-x+2;(2)6
【解析】试题分析:(1)由点A、B的横纵坐标结合反比例函数解析式即可得出点A、B的坐标,再由点A、B的坐标利用待定系数法即可得出直线AB的解析式;
(2)求出点C的坐标,利用三角形的面积公式结合A、B点的横坐标即可得出结论.
试题解析:(1)∵点A 、B在反比例函数y=-![]() 的图像上,
的图像上,
∴y=![]() =4 ,x=
=4 ,x=![]() =4,
=4,
∴A、B两点的坐标为A(-2,4),B(4,-2),
又 ∵A、B两点在一次函数y=kx+b 的图像上,
∴-2k+b=4且4k+b=-2,
解得:k=-1,b=2,
∴一次函数y=-x+2;
(2)直线y=-x+2与y轴的交点为C(0,2),
线段![]() 将△ABC分成△AOC和△BOC两个三角形,
将△ABC分成△AOC和△BOC两个三角形,
∴S△ABO=S△AOC+S△BOC=![]() ×2×2÷2+
×2×2÷2+![]() ×4×2=6.
×4×2=6.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角尺如图①摆放(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)点D为AB的中点,DE交AC于点P,DF经过点C.

(1)求∠ADE的度数;
(2)如图②,将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断
 的值是否随着α的变化而变化?如果不变,请求出
的值是否随着α的变化而变化?如果不变,请求出 的值;反之,请说明理由.
的值;反之,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.

(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图像经过点(-1.-5),且与正比例函数y=
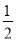 x的图象相交于点(2,m).
x的图象相交于点(2,m).(1)求m的值;
(2)求一次函数y=kx+b的解析式;
(3)求这两个函数图像与x轴所围成的三角形面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=60°,BE⊥AC,垂足为E,CF⊥AB,垂足为F,点D是BC的中点,BE,CF交于点M.
(1)如果AB=AC,求证:△DEF是等边三角形;
(2)如果AB≠AC,试猜想△DEF是不是等边三角形?如果△DEF是等边三角形,请加以证明;如果△DEF不是等边三角形,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学习了“展开与折叠”后,同学们了解了一些简单几何体的展开图,小明在家用剪刀剪一个如图(1)的长方体纸盒,但不小心多剪开了一条棱,得到图(2)中的纸片①和②,请解答下列问题:
(1)小明共剪开 条棱;
(2)现在小明想将剪断的纸片②拼接到纸片①上,构成该长方体纸盒的展开图,请你在①中画出纸片②的一种位置;
(3)请从A,B两题中任选一题作答.
A.若长方体纸盒的长,宽,高分别为m,m,n(单位:cm,m>n),求(2)中展开图的周长.
B.若长方体纸盒的长,宽,高分别是a,b,c(单位:cm,a>b>c),如图(3),画出它的展开图中周长最大时的展开图,并求出周长(用含a,b,c的式子表示)

相关试题

