搜索
【题目】如图，四边形ABCD中，AB=20，BC=15，CD=7，AD=24，∠B=90°．
（1）判断∠D是否是直角，并说明理由．
（2）求四边形ABCD的面积.
参考答案：
【答案】（1）∠D是直角（2）234
【解析】试题分析：（1）∠D是直角，连接AC．首先根据勾股定理求得AC的长，再根据勾股定理的逆定理求得∠D=90°即可；
（2）由题意可知四边形ABCD的面积等于两个直角三角形的面积问题的解．
试题解析：解：（1）∠D是直角．理由如下：
连接AC．∵AB=20，BC=15，∠B=90°，∴由勾股定理得AC2=202+152=625．
又∵CD=7，AD=24，∴CD2十AD2=625，∴AC2=CD2+AD2，∴∠D=90°，∴AD与CD垂直；
（2）四边形ABCD的面积=
ADDC+
ABBC=
×24×7+
×20×15=234．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在对第一章“丰富的图形世界”复习前，老师让学生整理正方体截面的形状并探究多面体（由若干个多边形所围成的几何体）的棱数、面数、顶点数之间的数量关系，如图是小颖用平面截正方体后剩余的多面体，请解答下列问题：
（1）根据上图完成下表：
多面体
V（顶点数）
F（面数）
E（棱数）
（1）
7
15
（3）
6
9
（5）
8
6
（2）猜想：一个多面体的V（顶点数），F（面数），E（棱数）之间的数量关系是 ；
（3）计算：已知一个多面体有20个面、30条棱，那么这个多面体有 个顶点．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）在如图所示的数轴上，把数﹣2，
，4，﹣
，2.5表示出来，并用“＜“将它们连接起来；（2）假如在原点处放立一挡板（厚度不计），有甲、乙两个小球（忽略球的大小，可看作一点），小球甲从表示数﹣2的点处出发，以1个单位长度/秒的速度沿数轴向左运动；同时小球乙从表示数4的点处出发，以2个单位长度/秒的速度沿数轴向左运动，在碰到挡板后即刻按原来的速度向相反的方向运动，设运动的时间为t（秒）．
请从A，B两题中任选一题作答．
A．当t=3时，求甲、乙两小球之间的距离．
B．用含t的代数式表示甲、乙两小球之间的距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将一副三角尺如图①摆放（在Rt△ABC中，∠ACB=90°，∠B=60°；在Rt△DEF中，∠EDF=90°，∠E=45°）点D为AB的中点，DE交AC于点P，DF经过点C．
（1）求∠ADE的度数；
（2）如图②，将△DEF绕点D顺时针方向旋转角α（0°<α<60°），此时的等腰直角三角尺记为△DE′F′，DE′交AC于点M，DF′交BC于点N，试判断
的值是否随着α的变化而变化？如果不变，请求出的值；反之，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数y=kx+b的图像经过点（－1．－5），且与正比例函数y=
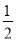x的图象相交于点（2，m）．（1）求m的值；
（2）求一次函数y=kx+b的解析式；
（3）求这两个函数图像与x轴所围成的三角形面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数y=kx+b 的图象与反比例函数y=
的图交象于A、B两点，且点A的横坐标和点B的纵坐标都是－2 ， 求：（1）一次函数的解析式；
（2）△AOB的面积
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在一次数学活动课上，张明用17个边长为1的小正方形搭成了一个几何体，然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体（不改变张明所搭几何体的形状），那么王亮至少还需要 个小立方体，王亮所搭几何体的表面积为 ．
相关试题
