【题目】如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察下列图形,并探究和解答下列问题:

(1)设铺设地面所用瓷砖的总块数为y,请写出y与n(表示第n个图形)的关系式;
(2)上述铺设方案,铺一块这样的长方形地面共用了506块瓷砖,求此时n的值;
(3)黑瓷砖每块4元,白瓷砖每块3元,在问题(2)中,共需要花多少钱购买瓷砖?
(4)否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算加以说明
参考答案:
【答案】(1)y=(n+3)(n+2);(2)20;(3)1604;(4)不存在
【解析】试题分析:(1)第1个图形有4×3块瓷砖,第2个图形有5×4块瓷砖,第3个图形有6×5块瓷砖,所以可以推出瓷砖的总块数为
y=(n+3)(n+2);
(2)当y=506时可以代入(1)中函数关系式求出n;
(3)和(1)一样可以推出白瓷砖的总块数为y'=(n+1)×n,然后可以推出黑瓷砖数目,再根据已知条件即可计算出钱数;
(4)利用(3)的结论计算即可判断是否存在.
试题解析:
(1)由题意,得y=(n+3)(n+2),即y=n2+5n+6,
∴y与n(n表示第n个图形)的函数关系式y=n2+5n+6;
(2)由题意,得n2+5n+6=506,解得n=20,
∴n=20;
(3)白瓷砖块数是n(n+1)=20(20+1)=420,黑瓷砖块数是506-420=86,
共需86×4+420×3=1604(元),
∴共需花1604元钱购买瓷砖;
(4)n(n+1)=n2+5n+6-n(n+1).
解得n=![]()
因为n不为整数.
∴不存在黑白瓷砖块数相等的情形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一元二次方程ax2﹣bx﹣2015=0有一根为x=﹣1,则a+b= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.
(1)求证:AD平分∠BAC;
(2)连接EF,求证:AD垂直平分EF.

-
科目: 来源: 题型:
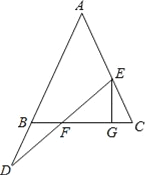
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.
(1)下列两个关系式:①DB=EC,②DF=EF,请你选择一个做为条件,另一个做为结论构成一个正确的命题,并给予证明.
你选择的条件是 ,结论是 .(只需填序号)
(2)在(1)的条件下,求证:FG=BC/2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】64的立方根是( )
A.4
B.±4
C.8
D.±8 -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形的对称轴的条数为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2
 ,延长AD到E,使AE=2AD,连接BE.
,延长AD到E,使AE=2AD,连接BE.(1)求证:△ABE为等边三角形;
(2)将一块含60°角的直角三角板PMN如图放置,其中点P与点E重合,且∠NEM=60°,边NE与AB交于点G,边ME与AC交于点F.求证:BG=AF;
(3)在(2)的条件下,求四边形AGEF的面积.

相关试题

