【题目】根据题意,解答问题:
(1)如图1,已知直线y=2x+4与x轴、y轴分别交于A、B两点,求线段AB的长.
(2)如图2,类比(1)的解题过程,请你通过构造直角三角形的方法,求出点M(3,4)与点N(﹣2,﹣1)之间的距离.
(3)在(2)的基础上,若有一点D在x轴上运动,当满足DM=DN时,请求出此时点D的坐标.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点D的坐标为(2,0).
;(3)点D的坐标为(2,0).
【解析】分析:(1)由一次函数解析式求得点A、B的坐标,则易求直角△AOB的两直角边OB、OA的长度,所以在该直角三角形中利用勾股定理即可求线段AB的长度;
(2)如图2,过M点作x轴的垂线MF,过N作y轴的垂线NE,MF和NE交于点C,构造直角△MNC,则在该直角三角形中利用勾股定理来求求点M与点N间的距离;
(3)如图3,设点D坐标为(m,0),连结ND,MD,过N作NG垂直x轴于G,过M作MH垂直x轴于H.在直角△DGN和直角△MDH中,利用勾股定理得到关于m的方程12+(m+2)=42+(3-m)2
通过解方程即可求得m的值,则易求点D的坐标.
详解:(1)令x=0,得y=4,即A(0,4).
令y=0,得x=-2,即B(-2,0).
在Rt△AOB中,根据勾股定理有:
AB=![]() ;
;
(2)如图2,过M点作x轴的垂线MF,过N作y轴的垂线NE,MF和NE交于点C.
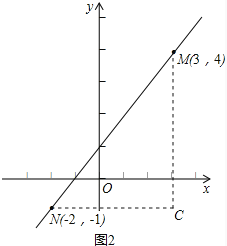
根据题意:MC=4-(-1)=5,NC=3-(-2)=5.
则在Rt△MCN中,根据勾股定理有:
MN=![]() ;
;
(3)如图3,设点D坐标为(m,0),连结ND,MD,

过N作NG垂直x轴于G,过M作MH垂直x轴于H.
则GD=|m-(-2)|,GN=1,DN2=GN2+GD2=12+(m+2)2
MH=4,DH=|3-m|,DM2=MH2+DH2=42+(3-m)2
∵DM=DN,
∴DM2=DN2
即12+(m+2)=42+(3-m)2
整理得:10m=20得m=2
∴点D的坐标为(2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(1,2),AB⊥x轴于点B,将△AOB绕点A逆时针旋转90°得到△ACD,双曲线y=
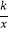 (x>0)恰好经过点C,交AD于点E,则点E的坐标为 .
(x>0)恰好经过点C,交AD于点E,则点E的坐标为 . 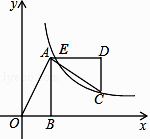
-
科目: 来源: 题型:
查看答案和解析>>【题目】李同学每天上学、放学使用公交卡乘坐公交车,公交卡的余额是100元.如果乘车次数用
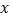 表示,公交卡上的余额用
表示,公交卡上的余额用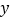 表示.
表示.次数
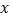
余额
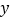 (元)
(元)1
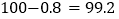
2
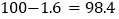
3
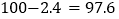
…
…
(1)请你根据表格中的信息,计算出第4次乘车后,公交卡上的余额;
(2)请你写出李同学公交卡上的余额
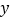 与乘车次数
与乘车次数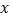 的关系式;
的关系式;(3)请帮李同学计算乘20次车后,公交卡上余额是多少元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算与解不等式组
(1)计算:|﹣2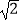 |﹣4sin45°+(3﹣π)°﹣(
|﹣4sin45°+(3﹣π)°﹣(  )﹣2;
)﹣2;
(2)解不等式组: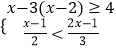 ,并在数轴上表示它的解集.
,并在数轴上表示它的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】有8袋枣林湾大枣,把每袋20千克作为标准,超过标准的千克数记为正,不足标准的千克数记为负,称后的记录如下:
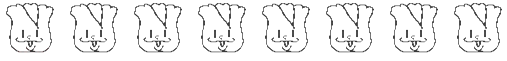
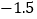
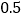
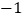
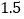
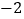
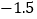
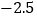
(1)这8袋大枣中,最接近20千克的那袋大枣为 千克;
(2)以每袋20千克为标准,这8袋大枣总计超过多少千克或不足多少千克?
(3)若每袋大枣每千克售价10元,则出售这8袋大枣可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张同学在计算
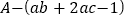 时,将“
时,将“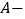 ”错看成了“
”错看成了“ ”,得出的结果是
”,得出的结果是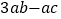 .
.(1)请你求出这道题的正确结果;
(2)试探索:当字母
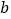 、
、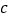 满足什么关系时,(1)中的结果与字母
满足什么关系时,(1)中的结果与字母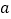 的取值无关.
的取值无关. -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到1h;②A,B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1小时后与摩托车相遇,此时距B地40千米.其中正确结论的个数是( )
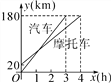
A. 2个 B. 3个 C. 4个 D. 1个
相关试题

