【题目】某中学六七年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.
(1)A、B型车每辆可分别载学生多少人?
(2)若租一辆A需要100元,一辆B需120元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.
参考答案:
【答案】(1)A、B型车每辆可分别载学生30人,40人;(2)租用1辆A型8辆B型车花费最少为1060元.
【解析】
(1)设A、B型车每辆可分别载学生x,y人,根据载客量,可得方程组![]() ,解方程组,可得答案;
,解方程组,可得答案;
(2)设租用A型a辆,B型b辆,根据题意列出方程:30a+40b=350求正整数解可得答案.
解:(1)设A、B型车每辆可分别载学生x,y人,
可得:![]() ,
,
解得:![]() ,
,
答:A、B型车每辆可分别载学生30人,40人;
(2)设租用A型a辆,B型b辆,
可得:30a+40b=350,
因为a,b为正整数,所以方程的解为: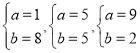 ,
,
方案一:A型1辆,B型8辆,费用:100×1+120×8=1060元;
方案二:A型5辆,B型5辆,费用:100×5+120×5=1100元;
方案三:A型9辆,B型2辆,费用:100×9+120×2=1140元;
所以租用1辆A型8辆B型车花费最少为1060元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是圆0直径BD延长线上的一点,点C在圆0上,AC=BC,AD=CD.
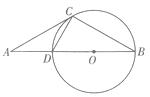
(1)求证:AC是圆0的切线;
(2)若⊙0的半径为2,求 ABC的面积.
ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(
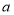 ,0),AB⊥
,0),AB⊥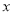 轴,且AB=10,点C(0,b),
轴,且AB=10,点C(0,b),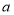 ,b满足
,b满足 .点P(t,0)是线段AO上一点(不包含A,O)
.点P(t,0)是线段AO上一点(不包含A,O)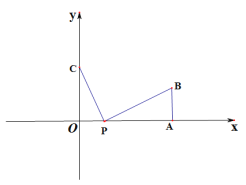
(1)当t=5时,求PB:PC的值;
(2)当PC+PB最小时,求t的值;
(3)请根据以上的启发,解决如下问题:正数m,n满足m+n=10,且正数
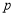 =
=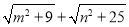 ,则正数
,则正数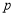 的最小值=________.
的最小值=________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,抛物线y=x2-+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
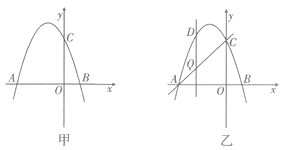
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且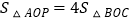 ,求点P的坐标;
,求点P的坐标;
(3)如图乙,设点Q是线段AC上的一动点,作DQ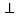 x轴,交抛物线于点D,求线段DQ长度的最大值.
x轴,交抛物线于点D,求线段DQ长度的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
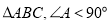 (如图),点
(如图),点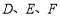 分别在边
分别在边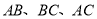 上,且四边形
上,且四边形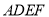 是菱形
是菱形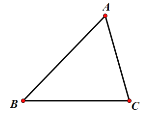
(1)请使用直尺与圆规,分别确定点
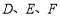 的具体位置(不写作法,保留画图痕迹);
的具体位置(不写作法,保留画图痕迹);(2)如果
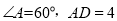 ,点
,点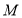 在边
在边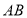 上,且满足
上,且满足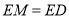 ,求四边形
,求四边形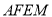 的面积;
的面积;(3)当
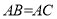 时,求
时,求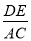 的值。
的值。
相关试题

