【题目】如图甲,抛物线y=x2-+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3).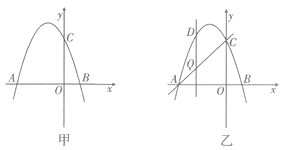
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且 ![]() ,求点P的坐标;
,求点P的坐标;
(3)如图乙,设点Q是线段AC上的一动点,作DQ ![]() x轴,交抛物线于点D,求线段DQ长度的最大值.
x轴,交抛物线于点D,求线段DQ长度的最大值.
参考答案:
【答案】
(1)解:把A(3,0),C(0,3)代入y=x2+bx+c ,
得 ![]() 解得
解得 ![]()
故该抛物线的解析式为:y=x22x+3 .
(2)解:设 ;P(x,x22x+3) ,由(1)知,该抛物线的解析式为y=x22x+3,则B(1,0).
∵S△AOP=4S△BOC ,
∴ ![]() ×3×|x22x+3|=4×
×3×|x22x+3|=4× ![]() ×1×3.
×1×3.
整理,得(x+1)2=0或x2+2x7=0,
解得x=1或x=1± ![]() .
.
则符合条件的点P的坐标为:(1,4)或(1+ ![]() ,4)或(1
,4)或(1 ![]() ,4) 。
,4) 。
(3)解:设直线AC的解析式为y=kx+t , 将A(3,0),C(0,3)代入,
得 ![]() 解得
解得 ![]()
即直线AC的解析式为y=x+3.
设Q点坐标为(x , x+3)(3≤x≤0),则D点坐标为(x , x22x+3),
QD=(x22x+3)(x+3)=x23x= ![]() +
+ ![]() ,
,
∴当x= ![]() 时,QD有最大值
时,QD有最大值 ![]() 。
。
【解析】(1)用待定系数法求出抛物线的解析式;
(2)设出P点的坐标,P(x,x22x+3) ,根据平抛物线的解析式求出其与x轴的另一个交点B的坐标,然后根据三角形的面积公式及S△AOP=4S△BOC , 列出关于x的一元二次方程![]() ×3×|x22x+3|=4×
×3×|x22x+3|=4× ![]() ×1×3;整理得到(x+1)2=0或x2+2x7=0,求解得出x的值,从而得出符合条件的点P的坐标;
×1×3;整理得到(x+1)2=0或x2+2x7=0,求解得出x的值,从而得出符合条件的点P的坐标;
(3)先用待定系数法求出直线AC的解析式,然后设出Q点坐标为(x , x+3)(3≤x≤0),则D点坐标为(x , x2![]() ) 2 +
) 2 + ![]() ,从而得出答案。
,从而得出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是圆0直径BD延长线上的一点,点C在圆0上,AC=BC,AD=CD.
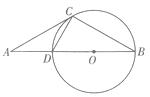
(1)求证:AC是圆0的切线;
(2)若⊙0的半径为2,求 ABC的面积.
ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学六七年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.
(1)A、B型车每辆可分别载学生多少人?
(2)若租一辆A需要100元,一辆B需120元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(
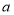 ,0),AB⊥
,0),AB⊥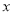 轴,且AB=10,点C(0,b),
轴,且AB=10,点C(0,b),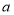 ,b满足
,b满足 .点P(t,0)是线段AO上一点(不包含A,O)
.点P(t,0)是线段AO上一点(不包含A,O)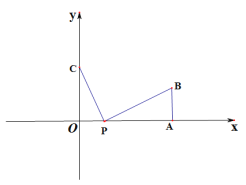
(1)当t=5时,求PB:PC的值;
(2)当PC+PB最小时,求t的值;
(3)请根据以上的启发,解决如下问题:正数m,n满足m+n=10,且正数
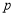 =
=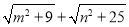 ,则正数
,则正数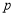 的最小值=________.
的最小值=________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
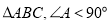 (如图),点
(如图),点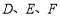 分别在边
分别在边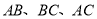 上,且四边形
上,且四边形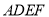 是菱形
是菱形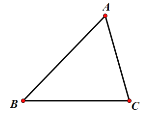
(1)请使用直尺与圆规,分别确定点
 的具体位置(不写作法,保留画图痕迹);
的具体位置(不写作法,保留画图痕迹);(2)如果
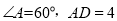 ,点
,点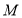 在边
在边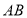 上,且满足
上,且满足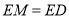 ,求四边形
,求四边形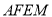 的面积;
的面积;(3)当
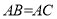 时,求
时,求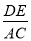 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则
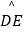 的长为( )
的长为( )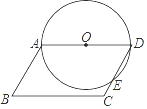
A. π
π
B. π
π
C. π
π
D. π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】为传播“绿色出行,低碳生活”的理念,小贾同学的爸爸从家里出发,骑自行车去图书馆看书,图1表达的是小贾的爸爸行驶的路程
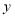 (米)与行驶时间
(米)与行驶时间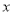 (分钟)的变化关系
(分钟)的变化关系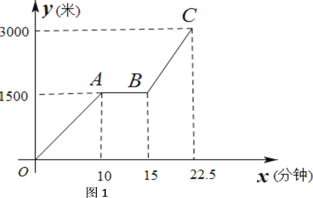
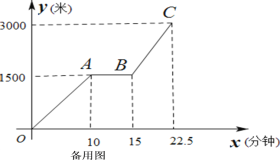
(1)求线段BC所表达的函数关系式;
(2)如果小贾与爸爸同时从家里出发,小贾始终以速度120米/分钟行驶,当小贾与爸爸相距100米是,求小贾的行驶时间;
(3)如果小贾的行驶速度是
 米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出
米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出 的取值范围。
的取值范围。
相关试题

