【题目】学生刘明,对某校六1班上学期期末的数学成绩(成绩取整数,满分为100分)作了统计,发现这个班每个人的成绩各不相同,并据此绘制成如下频数分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题:
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
频数 | 2 | 8 | 20 | a | 4 | c |
频率 | 0.04 | b | 0.40 | 0.32 | 0.08 | 1 |
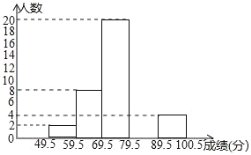
(1)频数、频率分布表中a=____,b=_____,c=_____;
(2)补全频数分布直方图;
(3)如果要画该班上学期期末数学成绩的扇形统计图,那么分数在69.5﹣79.5之间的扇形圆心角的度数是_______.
(4)张亮同学成绩为79分,他说:“我们班上比我成绩高的人还有![]() ,我要继续努力.”他的说法正确吗?请说明理由.
,我要继续努力.”他的说法正确吗?请说明理由.
参考答案:
【答案】(1)16、0.16、50;(2)补图见解析;(3)144°;(4)正确,理由见解析.
【解析】
(1)由69.5~79.5的频数及其频率可得总人数c,总人数乘以79.5~89.5的频率可得a,59.5~69.5的频数除以总人数可得b;
(2)由(1)所得结果可得;
(3)360°乘以分数在69.5-79.5之间的频率即可得;
(4)由表知比79分数高的是79.5~89.5、89.5~100.5这2组,将其频率相加可得所占比例,即可判断.
解:(1)∵调查的总人数c=20÷0.4=50,
∴a=50×0.32=16,b=8÷50=0.16,
故答案为:16、0.16、50;
(2)补全直方图如下:
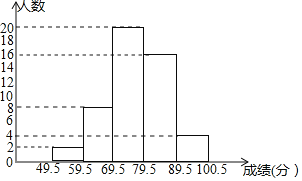
(3)分数在69.5﹣79.5之间的扇形圆心角的度数是360°×0.4=144°,
故答案为144°;
(4)正确.
由表可知,比79分高的人数占总人数的比例为0.32+0.08=0.4=![]() ,
,
∴他的说法正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)中的x与y的部分对应值如下表所示,则下列结论中,正确的个数有( )
x
-7
-6
-5
-4
-3
-2
y
-27
-13
-3
3
5
3
①当x<-4时,y<3②当x=1时,y的值为-13;③-2是方程ax2+(b-2)x+c-7=0的一个根;④方程ax2+bx+c=6有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
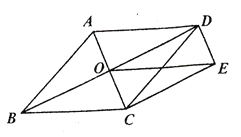
查看答案和解析>>【题目】如图,菱形
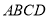 的对角线
的对角线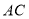 、
、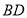 相交于点
相交于点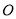 ,
,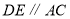 ,
,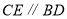 ,连接
,连接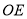 .
.
(1)求证:
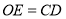 ;
;(2)探究:当
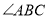 等于多少度时,四边形
等于多少度时,四边形 是正方形?并证明你的结论.
是正方形?并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是双曲线y=
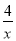 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】P是三角形
 内一点,射线PD//AC ,射线PB//AB .
内一点,射线PD//AC ,射线PB//AB .(1)当点D,E分别在AB,BC 上时,
①补全图1:
②猜想
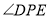 与
与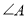 的数量关系,并证明;,
的数量关系,并证明;,
(2)当点
 都在线段
都在线段 上时,请先画出图形,想一想你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由
上时,请先画出图形,想一想你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由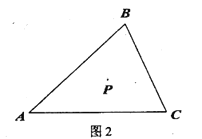
-
科目: 来源: 题型:
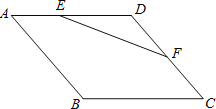
查看答案和解析>>【题目】如图,菱形ABCD的边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,且AE+CF=4,则△DEF面积的最大值为__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:

(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_ ▲ 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
相关试题

