【题目】已知二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴,并在所给坐标系中画出该函数的图象;
(3)该函数的图象经过怎样的平移得到y=x2的图象?

参考答案:
【答案】(1)b=-4,c=3;(2)顶点坐标为(2,﹣1),对称轴是直线x=2,图象见解析;(3)将该函数的图象向左平移2个单位,再向上平移1个单位得到y=x2的图象.
【解析】试题分析:(1)根据题意,将点(4,3),(3,0)分别代入二次函数解析式中,得二元一次方程组求解即可。
(2)由(1)可得二次函数解析式,将二次函数解析式化为顶点式即可。
(3)根据二次函数的顶点、对称轴、以及所过的点画出图象即可。
解:(1)将(4,3),(3,0)代入y=x2+bx+c,得![]() ,解得:
,解得:![]() ,
,
(2)二次函数y=x2﹣4x+3=(x﹣2)2﹣1,
则顶点坐标为(2,﹣1),对称轴是直线x=2,
如图,
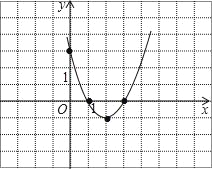
(3)将该函数的图象向左平移2个单位,再向上平移1个单位得到y=x2的图象.
点睛:本题是二次函数综合题,熟练掌握待定系数法求二次函数的解析式,二次函数一般式与顶点式的转化,二次函数的图像变化是解答本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.
(1)在正方形网格中,作出△AB1C1;
(2)设网格小正方形的边长为1,求旋转过程中动点B所经过的路径长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装着红、黄、绿三种只有颜色不同的球,其中红球有2个,黄球有1个,从中任意摸出1球是红球的概率为
 .
.(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB⊥AC,AB=2,AC=4.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转α°,分别交直线BC、AD于点E、F.

(1)当α= °,四边形ABEF是平行四边形;
(2)在旋转的过程中,从A、B、C、D、E、F中任意4个点为顶点构造四边形.
①α= °,构造的四边形是菱形;
②若构造的四边形是矩形,求出该矩形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是( )
A.
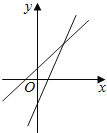 B.
B.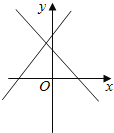
C.
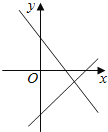 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )

A.
 B.
B. 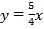 C.
C.  D.
D. 
相关试题

