搜索
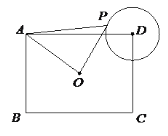
【题目】如图，在矩形ABCD中，AB=3，BC=4，O为矩形ABCD的中心，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP，则△AOP面积的最大值为（ ）
A. 4 B. 
C. 
D. 
参考答案：
【答案】D
【解析】解：当P点移动到平行于OA且与⊙D相切时，△AOP面积的最大，如图，∵P是⊙D的切线，∴DP垂直与切线，延长PD交AC于M，则DM⊥AC，∵在矩形ABCD中，AB=3，BC=4，∴AC= 
=5，∴OA= 
，∵∠AMD=∠ADC=90°，∠DAM=∠CAD，∴△ADM∽△ACD，∴
，∵AD=4，CD=3，AC=5，∴DM= 
，∴PM=PD+DM=1+ 
= 
，∴△AOP的最大面积= 
OAPM= 
= 
，故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC三个顶点的坐标分别为A（1，1）、B（4，2）、C（3，4）．
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1；
(2)请画出△ABC关于x轴对称的△A2B2C2三个顶点A2、B2、C2的坐标；
(3)在x轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两人分别从相距100km的A、B两地同时出发相向而行,并以各自的速度匀速行驶．甲出发2h后到达B地立即按原路返回，返回时速度提高了30km/h，回到A地后在A地休息等乙，乙在出发5h后到达A地．(友情提醒：可以借助用线段图分析题目）
（1）乙的速度是_______
，甲从A地到B地的速度是_______，甲在出发_______小时到达A地．（2）出发多长时间两人首次相遇？
（3）出发多长时间时，两人相距30千米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，
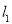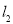分别表示使用一种白炽灯和一种节能灯的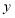费用
（费用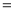
灯的售价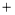
电费，单位：元）与照明时间
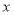（小时）的函数图象，假设两种灯的使用寿命都是
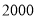小时，照明效果一样.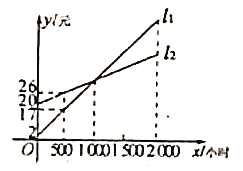
（1）根据图象分别求出
，的函数表达式；（2）小亮认为节能灯一定比白炽灯省钱，你是如何想的？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点
是等边
内一点，
，
，将
绕点
顺时针方向旋转
得到
，连接
，
.
（1）当
时，判断
的形状，并说明理由；（2）求
的度数；（3）请你探究：当
为多少度时，是等腰三角形？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知反比例函数y=
（x＞0）与正比例函数y=x（x≥0）的图象，点A（1，5）、点A′（5，b）与点B′均在反比例函数的图象上，点B在直线y=x上，四边形AA′B′B是平行四边形，则B点的坐标为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个自然数的立方，可以分裂成若干个连续奇数的和．例如：23，33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和，即23=3+5；33=7+9+11；43=13+15+17+19；…；若103也按照此规律来进行“分裂”，则103“分裂”出的奇数中，最小的奇数是_________
相关试题
