【题目】一元二次方程ax2+x﹣2=0有两个不相等实数根,则a的取值范围是( )
A.a ![]()
B.a= ![]()
C.a ![]() 且a≠0
且a≠0
D.a ![]() 且a≠0
且a≠0
参考答案:
【答案】C
【解析】解:∵一元二次方程ax2+x﹣2=0有两个不相等实数根,
∴b2﹣4ac=12﹣4a(﹣2)>0,
解得:a>﹣ ![]() 且a≠0,
且a≠0,
故选C.
【考点精析】本题主要考查了一元二次方程的定义和求根公式的相关知识点,需要掌握只有一个未知数,并且未知数的项的最高系数为2的方程为一元二次方程;根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年深圳国际马拉松赛于12月7日拉开帷幕,某马拉松爱好者用无人机拍摄比赛过程.如图,在无人机的镜头C下,观测深南大道A处的俯角为30°,B处的俯角为45°.如果此时无人机镜头C处离路面的高度CD为100米,点A、D、B在同一直线上,求A、B两处之间的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD中,AB=6,∠B=60°.E是BC边上一动点,F是CD边上一动点,且BE=CF,连接AE、AF.
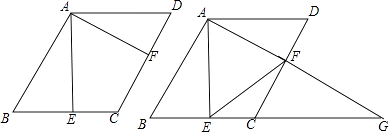
(1)∠EAF的度数是;
(2)求证:AE=AF;
(3)延长AF交BC的延长线于点G,连接EF,设BE=x,EF2=y,求y与x之间的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线l:y=﹣x+2与x轴交于点A、与y轴交于点B.抛物线y=ax2+bx+c(a≠0)经过O、A两点,与直线l交于点C,点C的横坐标为﹣1.

(1)求该抛物线的函数表达式;
(2)若点P是位于直线l下方抛物线上的一个动点,且不与点A、点C重合,连接PA、PC.设△PAC的面积为S,求当S取得最大值时点P的坐标,并求S的最大值;
(3)如图2,设抛物线的顶点为D,连接AD、BD.点E是对称轴m上一点,F是抛物线上一点,请直接写出当△DEF与△ABD相似时点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC和△DBE均为等腰直角三角形.
(1)求证:AD=CE;
(2)求证:AD和CE垂直.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,BC=3,则tan∠ACD的值为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A是双曲线y=
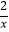 (x>0)上一点,过点A作AB∥x轴,交双曲线y=﹣
(x>0)上一点,过点A作AB∥x轴,交双曲线y=﹣ 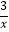 (x<0)于点B,若OA⊥OB,则
(x<0)于点B,若OA⊥OB,则 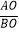 的值为( )
的值为( ) 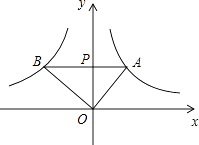
A.
B.
C.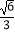
D.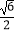
相关试题

