搜索
【题目】如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，若AC=4，BC=3，则tan∠ACD的值为（ ） 
A.
B.
C.
D.
参考答案：
【答案】A
【解析】解：∵在Rt△ABC中，∠ACB=90°，CD⊥AB于D，
∴∠CDA=90°，∠A+∠B=90°，
∴∠A+∠ACD=90°，
∴∠B=∠ACD，
∵在Rt△ABC中，∠ACB=90°，AC=4，BC=3，tanB= 
，
∴tanB= 
，
∴tan∠ACD= ，
故选A．
【考点精析】根据题目的已知条件，利用解直角三角形的相关知识可以得到问题的答案，需要掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知直线l：y=﹣x+2与x轴交于点A、与y轴交于点B．抛物线y=ax2+bx+c（a≠0）经过O、A两点，与直线l交于点C，点C的横坐标为﹣1．
（1）求该抛物线的函数表达式；
（2）若点P是位于直线l下方抛物线上的一个动点，且不与点A、点C重合，连接PA、PC．设△PAC的面积为S，求当S取得最大值时点P的坐标，并求S的最大值；
（3）如图2，设抛物线的顶点为D，连接AD、BD．点E是对称轴m上一点，F是抛物线上一点，请直接写出当△DEF与△ABD相似时点E的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一元二次方程ax2+x﹣2=0有两个不相等实数根，则a的取值范围是（ ）
A.a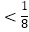
B.a=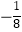
C.a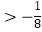
且a≠0
D.a
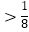且a≠0 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，△ABC和△DBE均为等腰直角三角形．
（1）求证：AD=CE；
（2）求证：AD和CE垂直．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A是双曲线y=
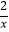（x＞0）上一点，过点A作AB∥x轴，交双曲线y=﹣ 
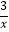（x＜0）于点B，若OA⊥OB，则 
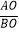的值为（ ）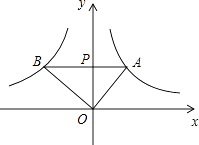 
A.
B.
C.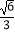
D.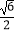
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列结论：
①abc＜0；②b2﹣4ac＞0；③3a+c＜0；④16a+4b+c＞0．
其中正确结论的个数是（ ）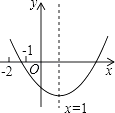
A.1个
B.2个
C.3个
D.4个 -
科目： 来源： 题型：
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”，计划将某村的居民自来水管道进行改造．该工程若由甲队单独施工恰好在规定时间内完成；若乙队单独施工，则完成工程所需天数是规定天数的1.5倍．如果由甲、乙队先合做15天，那么余下的工程由甲队单独完成还需5天．
（1）这项工程的规定时间是多少天？
（2）已知甲队每天的施工费用为6500元，乙队每天的施工费用为3500元．为了缩短工期以减少对居民用水的影响，工程指挥部最终决定该工程由甲、乙队合做来完成．则该工程施工费用是多少？
相关试题
