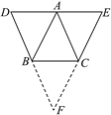
【题目】如图所示,已知BD∥AC,CE∥BA,且点D,A,E在一条直线上,设∠BAC=x,∠D+∠E=y.
(1)试用含x的代数式表示y;
(2)当x=90°时,判断直线DB与直线EC的位置关系,并说明理由.

参考答案:
【答案】(1)y=180°-x(0°<x<180°);(2)DB⊥EC.理由见解析.
【解析】
(1)根据两直线平行,同位角相等可得∠EAC =∠D,∠DAB =∠E,再根据平角等于180°列式整理即可得解;
(2)延长DB,EC交于点F,由BD∥AC,推出∠BAC=∠DBA.因为x=90°所以∠DBA=90°结合CE∥BA,可证DB⊥EC.
(1)y=180°-x(0°<x<180°).
(∵BD∥AC,CE∥BA,
∴∠EAC=∠D,∠DAB=∠E,
∵D、A.E在同一条直线上,
∴∠EAC +∠BAC+∠DAB =180°,
∵∠BAC=x,∠D+∠E=y,
∴x+y=180°,
∴y=180°x.)
(2)DB⊥EC.理由:如图,延长DB,EC交于点F.
∵BD∥AC,
∴∠BAC=∠DBA.
∵x=90°,即∠BAC=90°,
∴∠DBA=90°.
∵CE∥BA,
∴∠DFE=∠DBA=90°,
∴DB⊥EC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线 y=
 x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).
x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).(1)当 x =______________时,PB+PC 的值最小;
(2)当 x =______________时,|PB-PC|的值最大.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2﹣4x﹣2经过A,B两点.
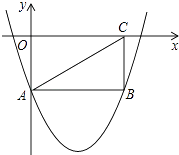
(1)求A点坐标及线段AB的长;
(2)若点P由点A出发以每秒1个单位的速度沿AB边向点B移动,1秒后点Q也由点A出发以每秒7个单位的速度沿AO,OC,CB边向点B移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒.
①当PQ⊥AC时,求t的值;
②当PQ∥AC时,对于抛物线对称轴上一点H,∠HOQ>∠POQ,求点H的纵坐标的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,完成下列推理:

∵∠1=∠2(已知),
∴________∥________(__________________________).
∵∠2=∠3(已知),
∴________∥________(___________________________),
∴________∥________(___________________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数 y=kx+4(k≠0).
(1)当 x=-1 时,y=2,求此函数的表达式;
(2)函数图象与 x 轴、y 轴的交点分别为 A、B, 求出△AOB 的面积;
(3)利用图象求出当 y≤3 时,x 的取值范围.
-
科目: 来源: 题型:
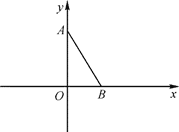
查看答案和解析>>【题目】如图,平面直角坐标系 xOy 中,已知点 A(0,3),点 B(
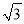 ,0),连接 AB.若对于平 面内一点 C,当△ABC 是以 AB 为腰的等腰三角形时,称点 C 是线段 AB 的“等长点”
,0),连接 AB.若对于平 面内一点 C,当△ABC 是以 AB 为腰的等腰三角形时,称点 C 是线段 AB 的“等长点”(1)在点 C1 (-2,
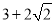 ),点 C2 (0,-2),点 C3 (
),点 C2 (0,-2),点 C3 (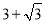 ,
, 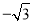 )中,线段 AB 的“等长点”是点______________;
)中,线段 AB 的“等长点”是点______________;(2)若点 D( m , n )是线段 AB 的“等长点”,且∠DAB=60,求 m 和 n 的值.
相关试题

