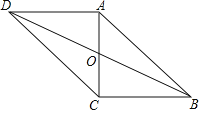
【题目】如图,在ABCD中,对角线AC、BD交于点O,AC⊥BC,且ABCD的周长为36,△OCD的周长比△OBC的周长大2.
(1)求BC,CD的长;
(2)求ABCD的面积.
参考答案:
【答案】(1)BC=8,CD=10;(2)48.
【解析】
(1)因为AD=BC,AB=CD,OA=OC,求出DC+BC=18,DC-BC=2,解方程组即可得出答案.
(2)利用勾股定理可求出AC的长,进而可求出ABCD的面积.
(1)∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,AO=OC,
∵平行四边形ABCD的周长为18,
∴DC+BC=18①,
∵△OCD的周长比△OBC的周长大2,
∴(CD+OD+OC)-(BC+OB+OC)=2,
∴CD-BC=2②,
①+②得:2CD=20,
CD=10,
①-②得:2BC=16,
BC=8;
(2)∵BC=8,AB=CD=10,AC⊥BC,
∴AC=![]() =6,
=6,
∴ABCD的面积=6×8=48.
-
科目: 来源: 题型:
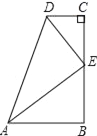
查看答案和解析>>【题目】在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点
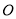 为坐标原点,点
为坐标原点,点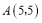 为第一象限内一点,点
为第一象限内一点,点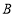 在
在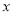 轴正半轴上,且
轴正半轴上,且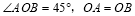 .
.
(1)求点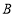 的坐标;
的坐标;
(2)动点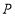 以每秒2个单位长度的速度,从点
以每秒2个单位长度的速度,从点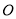 出发,沿
出发,沿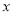 轴正半轴匀速运动,设点
轴正半轴匀速运动,设点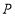 的运动时间为
的运动时间为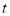 秒,
秒,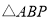 的面积为
的面积为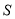 ,请用含有
,请用含有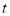 的式子表示
的式子表示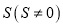 ,并直接写出
,并直接写出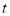 的取值范围;
的取值范围;
(3)如图2,在(2)的条件下,点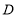 坐标为
坐标为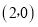 ,连接
,连接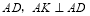 ,过点
,过点 作
作 轴的垂线交
轴的垂线交 于点
于点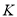 ,过点
,过点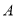 作
作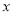 轴的平行线
轴的平行线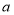 ,在点
,在点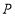 的运动过程中,直线
的运动过程中,直线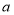 上是否存在一点
上是否存在一点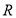 ,使
,使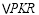 是以
是以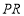 为腰的等腰直角三角形?若存在,求出点
为腰的等腰直角三角形?若存在,求出点 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.
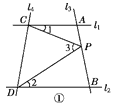
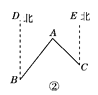
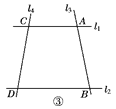
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一定范围内,弹簧的长度x(cm)与它所挂物体的重量y(g)之间满足关系式y=kx+b.已知挂重为50 g时,弹簧长12.5 cm;挂重为200 g时,弹簧长20 cm;那么当弹簧长15 cm时,挂重为( )
A. 80 g B. 100 g C. 120 g D. 150 g
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中: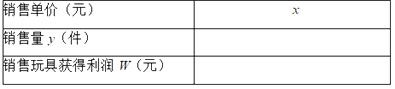
(2)在(1)条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

相关试题

