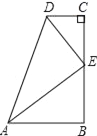
【题目】在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是_____.
参考答案:
【答案】35°
【解析】
过点E作EF⊥AD于F,根据角平分线上的点到角的两边的距离相等可得CE=EF,再根据到角的两边距离相等的点在角的平分线上可得AE是∠BAD的平分线,然后求出=∠AEB,再根据直角三角形两锐角互余求解即可.
过点E作EF⊥AD于F,
∵DE平分∠ADC,
∴CE=EF,
∵E是BC的中点,
∴CE=BE,
∴BE=EF,
∴AE是∠BAD的平分线,
∵∠CED=35°,
∴∠AEB=90°﹣∠CED=90°﹣35°=55°,
∵∠B=90°,
∴∠EAB=90°﹣55°=35°,
故答案为:35°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).

(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
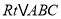 中,
中,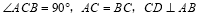 于点
于点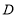 ,点
,点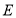 是射线
是射线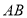 上一点,连接
上一点,连接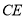 ,过点
,过点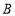 作
作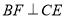 于点
于点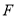 ,且交直线
,且交直线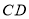 于点
于点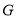 .
.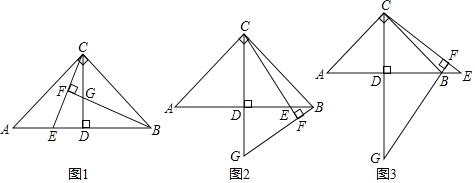
(1)如图1,当点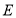 在线段
在线段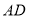 上时,求证:
上时,求证: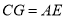 .
.
(2)如图2,当点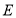 在线段
在线段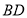 上时,其它条件不变,请猜想
上时,其它条件不变,请猜想 与
与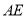 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)如图3,当点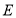 在线段
在线段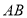 的延长线上时,其它条件不变,请直接写出
的延长线上时,其它条件不变,请直接写出 与
与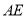 之间的数量关系.
之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点
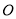 为坐标原点,点
为坐标原点,点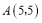 为第一象限内一点,点
为第一象限内一点,点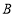 在
在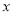 轴正半轴上,且
轴正半轴上,且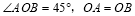 .
.
(1)求点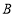 的坐标;
的坐标;
(2)动点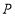 以每秒2个单位长度的速度,从点
以每秒2个单位长度的速度,从点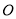 出发,沿
出发,沿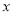 轴正半轴匀速运动,设点
轴正半轴匀速运动,设点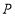 的运动时间为
的运动时间为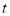 秒,
秒,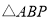 的面积为
的面积为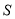 ,请用含有
,请用含有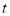 的式子表示
的式子表示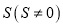 ,并直接写出
,并直接写出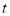 的取值范围;
的取值范围;
(3)如图2,在(2)的条件下,点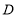 坐标为
坐标为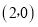 ,连接
,连接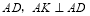 ,过点
,过点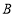 作
作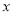 轴的垂线交
轴的垂线交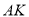 于点
于点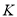 ,过点
,过点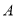 作
作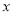 轴的平行线
轴的平行线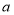 ,在点
,在点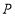 的运动过程中,直线
的运动过程中,直线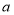 上是否存在一点
上是否存在一点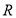 ,使
,使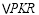 是以
是以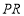 为腰的等腰直角三角形?若存在,求出点
为腰的等腰直角三角形?若存在,求出点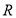 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.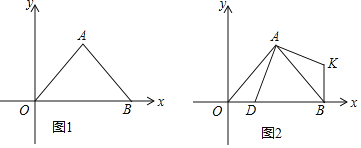
-
科目: 来源: 题型:
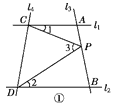
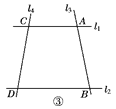
查看答案和解析>>【题目】如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
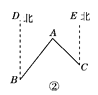
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.
-
科目: 来源: 题型:
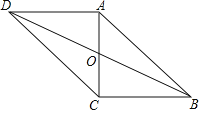
查看答案和解析>>【题目】如图,在ABCD中,对角线AC、BD交于点O,AC⊥BC,且ABCD的周长为36,△OCD的周长比△OBC的周长大2.
(1)求BC,CD的长;
(2)求ABCD的面积.
相关试题

